逻辑回归 Logistic Regression
函数Function
由先验事件,我们可以得到逻辑回归的函数:
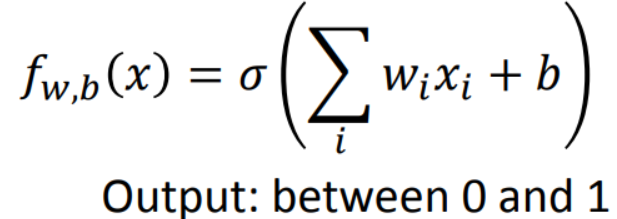
其通过图的形式可以表示成如下:
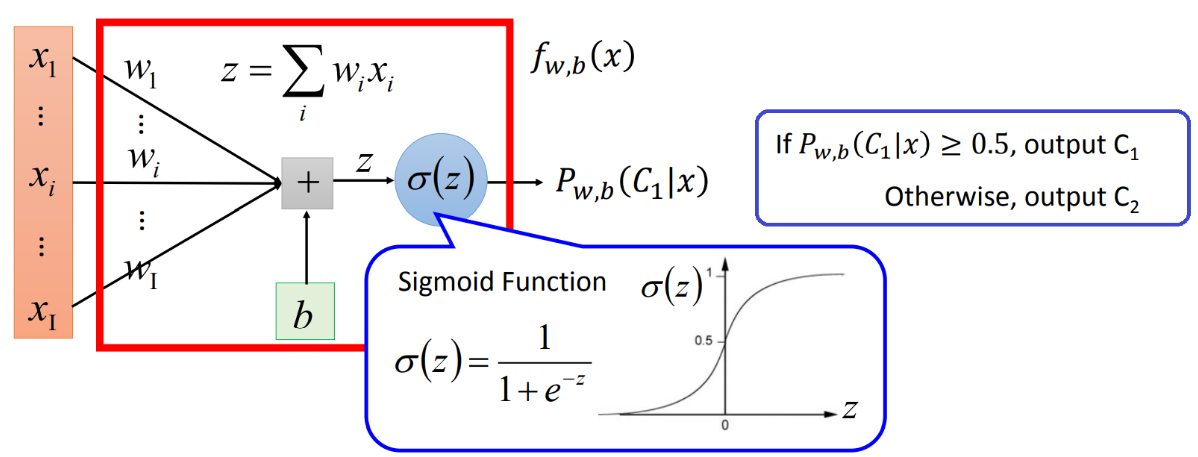
损失函数Loss
损失函数的定义为$L(w,b)$是样本集通过Function预测发生其对应事件的最大可能性。 则可以将Loss定义为如下:

这里有个小技巧,有利于Gradient Descent求微分,具体如下:

优化Optimization
通过上述的定义,我们可以轻松求Loss的微分,并且最终的结果也产生实际意义:

这里思考一下,如果Loss不使用Cross Entropy而是使用MSE,则在微分时得到如下结果:

这样的结果显然不利于梯度下降,并且我们可以比较它们的Loss曲线看出:
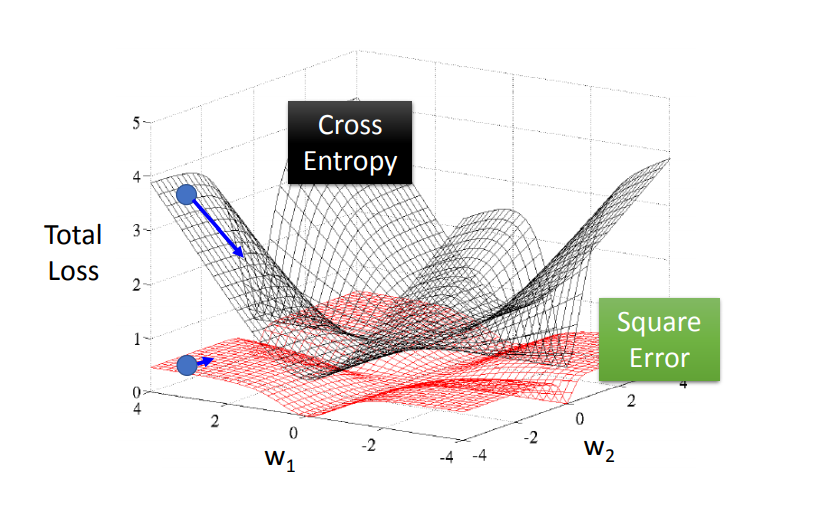
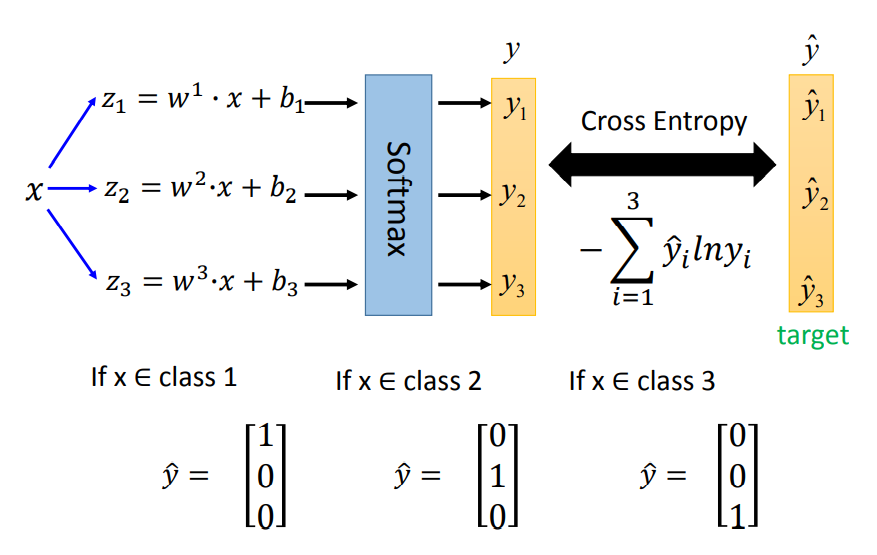
多分类器Multi-class Classification
多分类其的函数定义可以借鉴Binary Classification,其最后需要引用softmax以便使不同结果的差距放大。
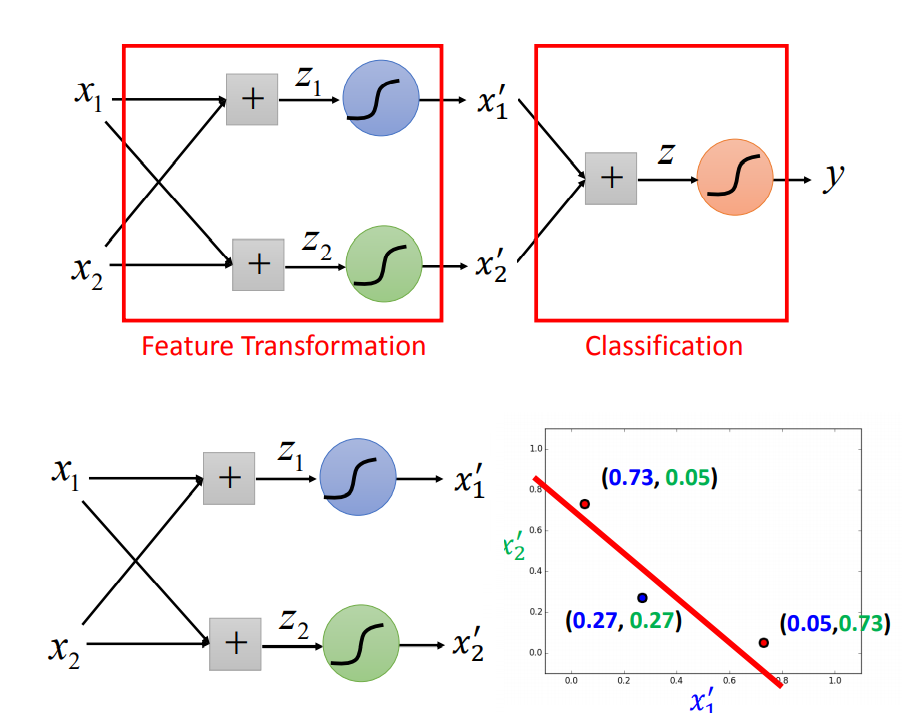
但是,逻辑回归仍然存在如下问题,如下的分类任务无法很好的用一条直线进行划分:
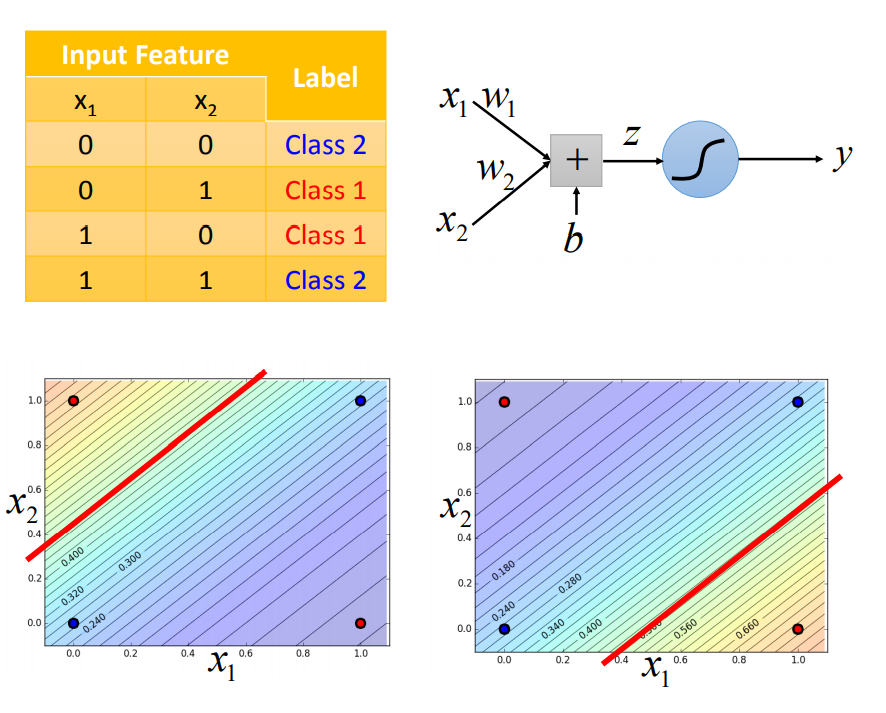
因此,我们可以尝试将样本点进行线性变化后,再进行分类,其过程就变成如下这样: