梯度下降 Gradient Descent
Gradient Descent的数学证明
根据多元泰勒展开式,当$(x,y)$无限接近$(x_0,y_0)$时,省略皮亚诺余项,$h(x,y)$可以表示为:
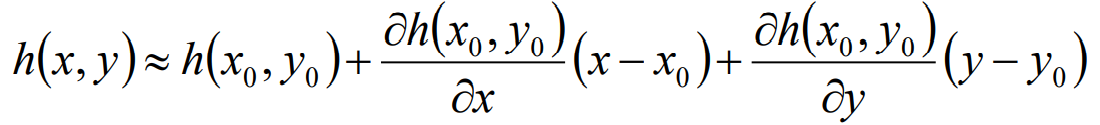
由上式可以得到损失函数在某点$L(a,b)$的邻域内,$L(\theta)$可以近似的表示为如下:
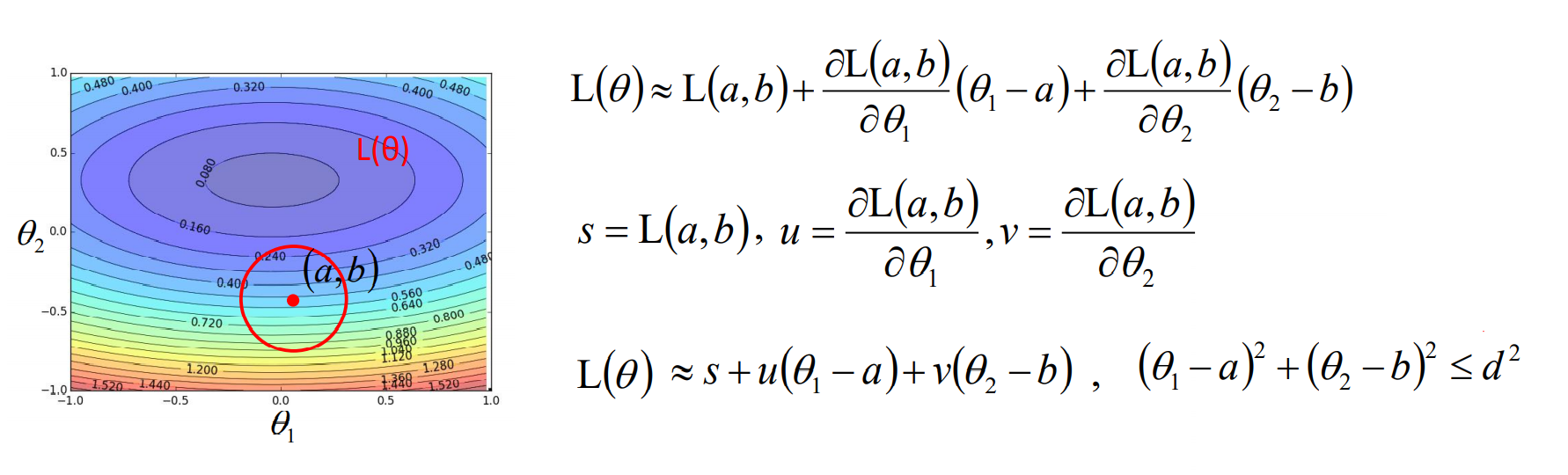
为了使$L(\theta)$变小,可以将$L(\theta)$写成两个向量内积形式,则当两个向量反向且$(\Delta \theta_1,\Delta \theta_2)$刚好达到邻域边界时,可保证$L(\theta)$
取得最小值:
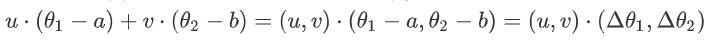

其中我们可以看到,当$\eta$(learning rate)太大超过了邻域时,就会超出泰勒公式$L(\theta)$的近似区间,此时并不能保证梯度下降的正确性。
Critical Point问题
Critical Point通俗的将,就是Loss Function下降到某个位置不能再继续下降了(各维度的微分都为零)导致的现象。
Critical Point可以分为:
- Local Minima: 局部最小值
- Saddle Point: 鞍点
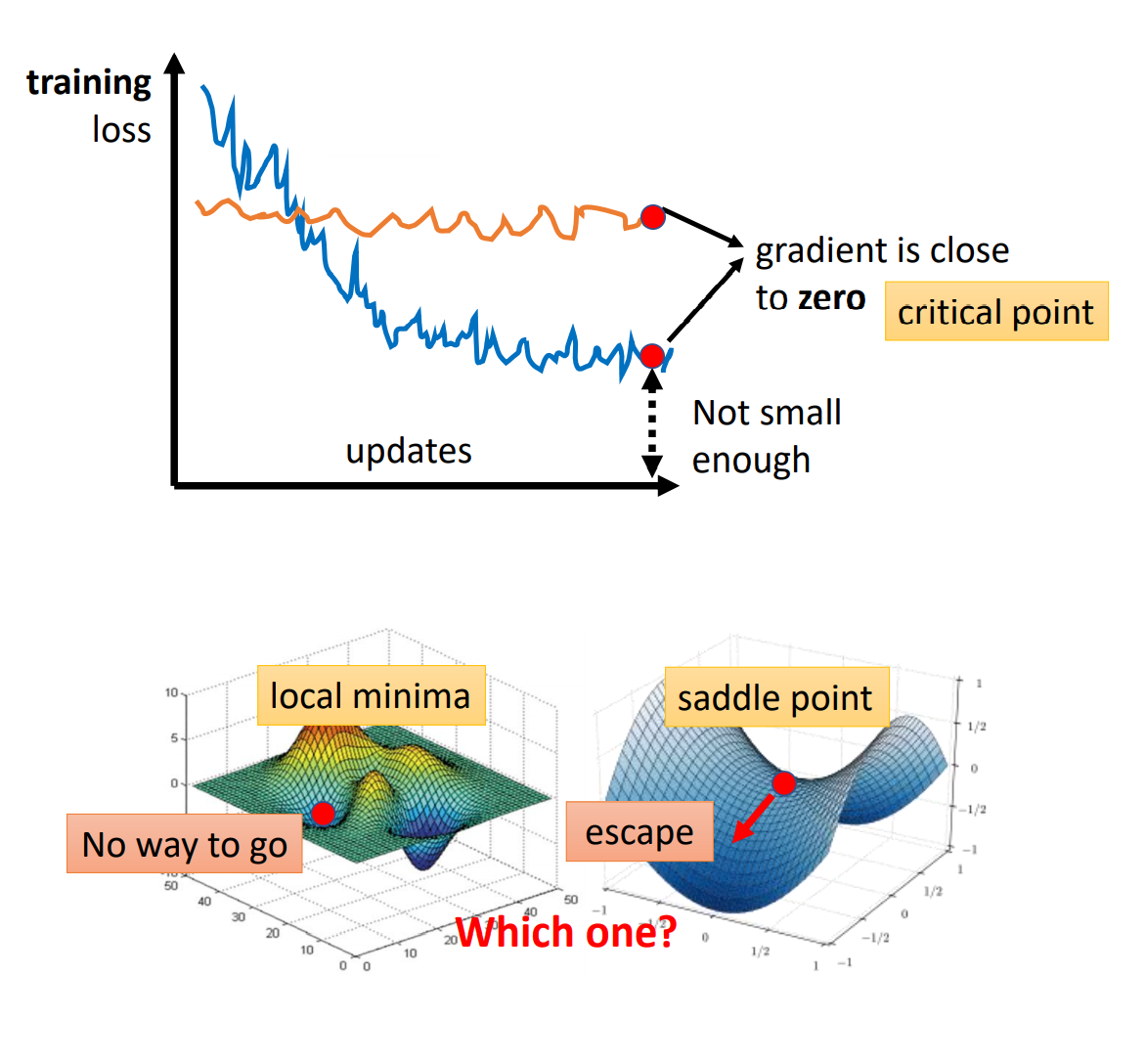
接下来我们将从数学角度讨论如何判别Critical Point是Local Minima还是Saddle Point。
判别Local Minima / Saddle Point
利用多元泰勒展开式,当我们下降到$\theta'$的时候,$L(\theta)$在$\theta'$的一个很小的邻域范围内,可以近似表示成:
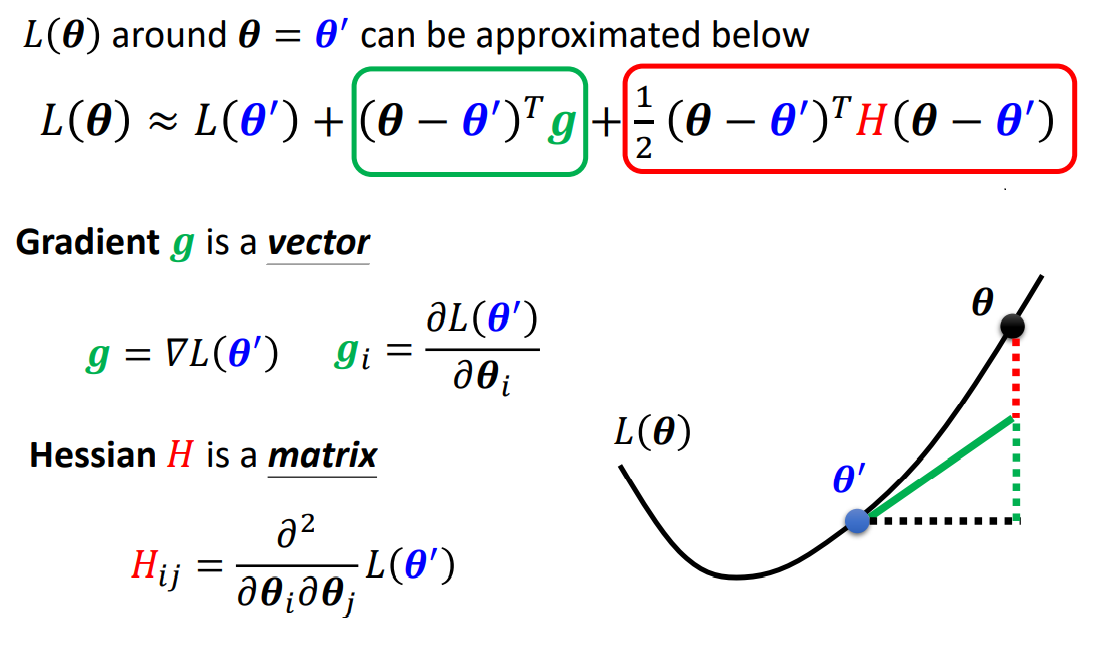
此时在Saddle Point处,一阶微分均为零,则$L(\theta)$又可以被近似的表示成:
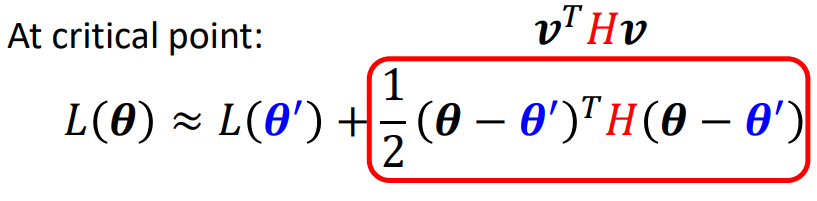
到此位置,利用线性代数的二次型理论,我们可以利用矩阵$H$的特征值讨论后项是恒正恒负,以此判别Local Minima / Saddle Point。

若二次型理论遗忘,可见下列的结论即可:

Saddle Point处怎么下降
上图泰勒展开式中,观察最后一项,怎么找一个$\theta$使它为负数,即可使$L(\theta)<L(\theta')$即可。

Learning Rate问题
Learning Rate过高或过低带来的问题
- Learning Rate very large: 如上节证明,不能保证泰勒定义的近似性,因此不保证梯度下降的正确性;
- Learning Rate very small: 下降的速度太慢了,需要很久达到Loss的最小值。
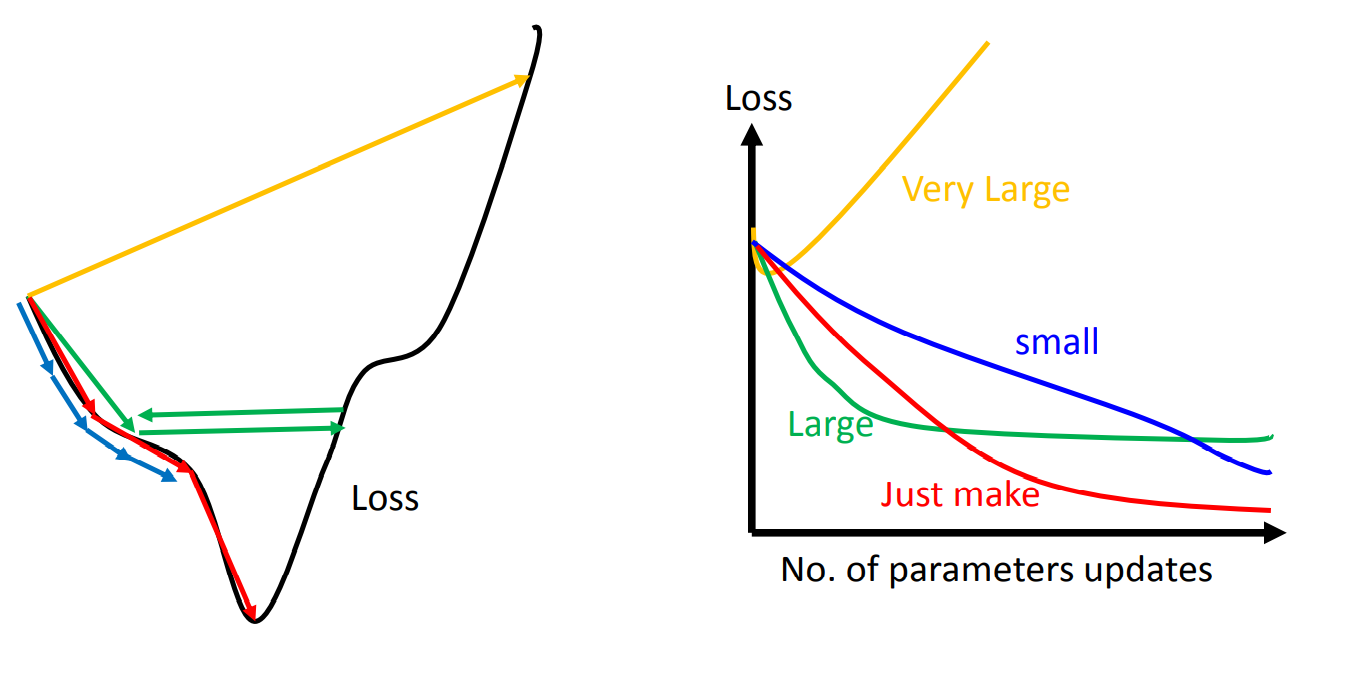
如何动态调整Learning Rate
动态调整Learning Rate在于: 前期下降更快,而后期接近最小损失时下降尽可能减缓。
最基本、最简单的大原则是:Learning Rate通常是随着参数的更新越来越小的
这里我们逐步引入各种Optimization优化器进行比较
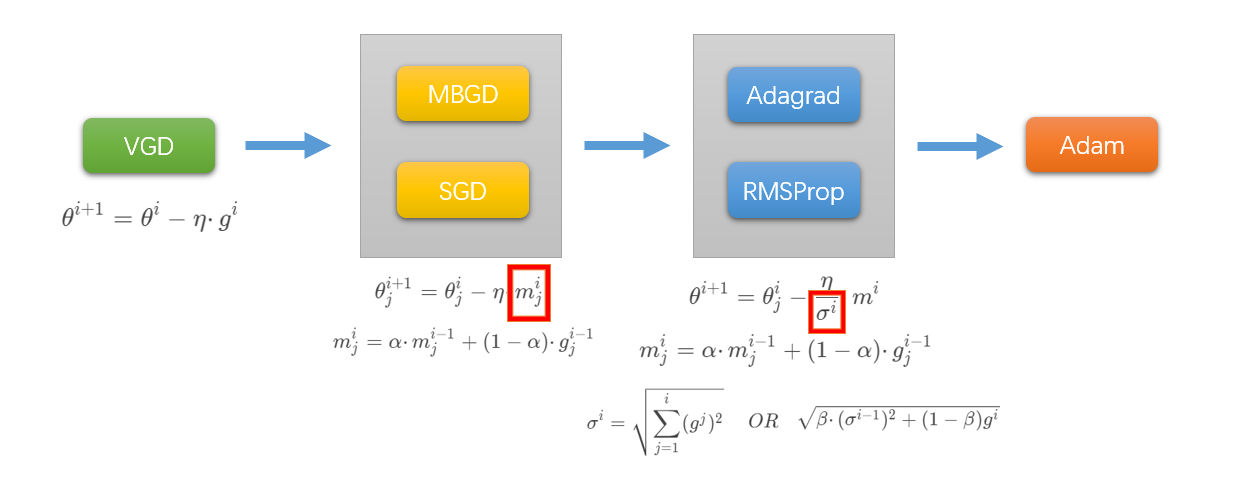
VGD (Vanilla Gradient Descent)
(Vanilla) Gradient Descent 是我们认为最一般的梯度下降法。

MBGD & SGD
- MBGD: Mini-Batch Gradient Descent
- SGD: Stochastic Gradicent Descent
相对于一般的VGD梯度下降法,小批量梯度下降在于对每个小的Batch计算微分后,就立刻更新$\theta$,可以更快的进行下降。
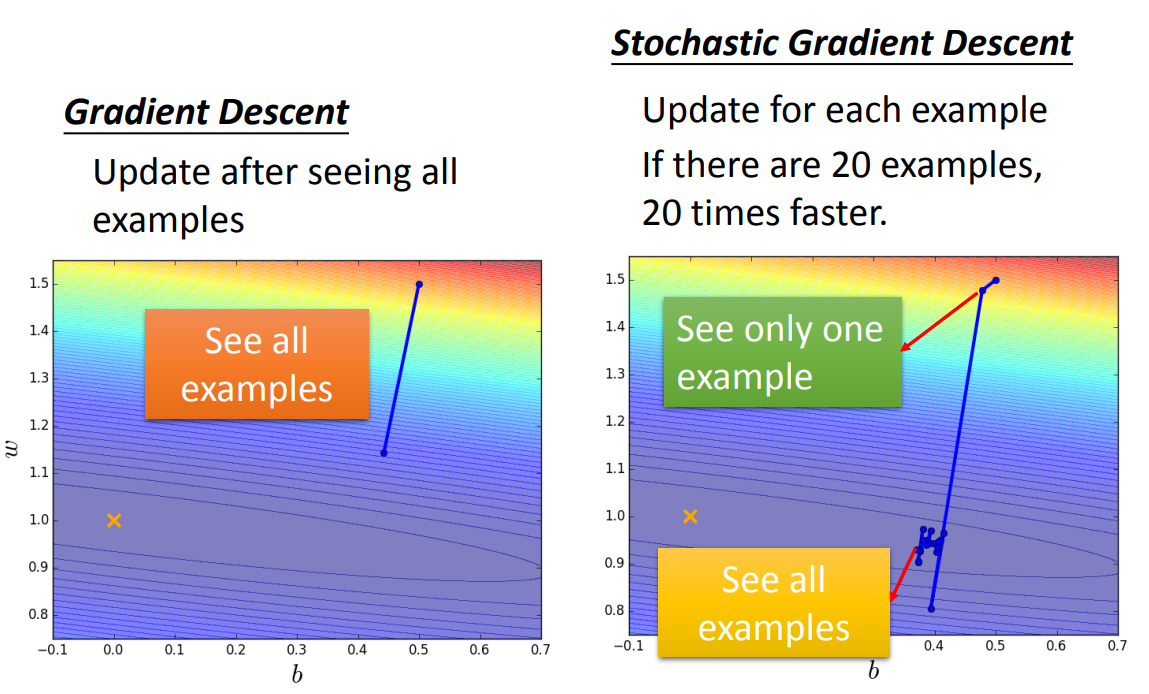
随机梯度下降SGD是对Mini-Batch Loss的实现方法可以让训练更快速,传统的Gradient Descent的思路是看完所有的样本点之后再构建Loss Function,然后去更新参数;而Stochastic
Gradient Descent的做法是,看到一个样本点就更新一次,因此它的Loss Function不是所有样本点的Error平方和,而是这个随机样本点的Error平方。

经历一次样本更新后,Stochastic Gradient Descent与传统Gradient Descent的效果对比如下:
Adagrad
Adagrad是最原始的自适应梯度下降算法,Adagrad需要解决如下问题:
对于一个Function,其Loss Function在Trainning Set上不断下降的训练过程中,可能最终会出现Loss无法继续下降的现象。
该问题未必是由于遇到Critical Point(Local Minima/Saddle Point)导致的,下图给出一个具体的例子:

(Ratio:正负特征值的笔直。特征值指的是对于Local Minima的判别,具体参照上节Critical Point的介绍。简单地说是通过Loss Function在某一点处矩阵表示的泰勒公式中,二阶导数构成矩阵的特征值进行判别。)
而导致Loss无法继续下降的原因大多是因为Optimization自身出现了问题。
- 问题:
Larning Rate太大,导致每次更新的步长太大。
对于不同的维度feature,设置不同的Learning Rate,并且让Learning Rate可以根据之前的Gradient梯度下降值动态变化,具体方式如下:
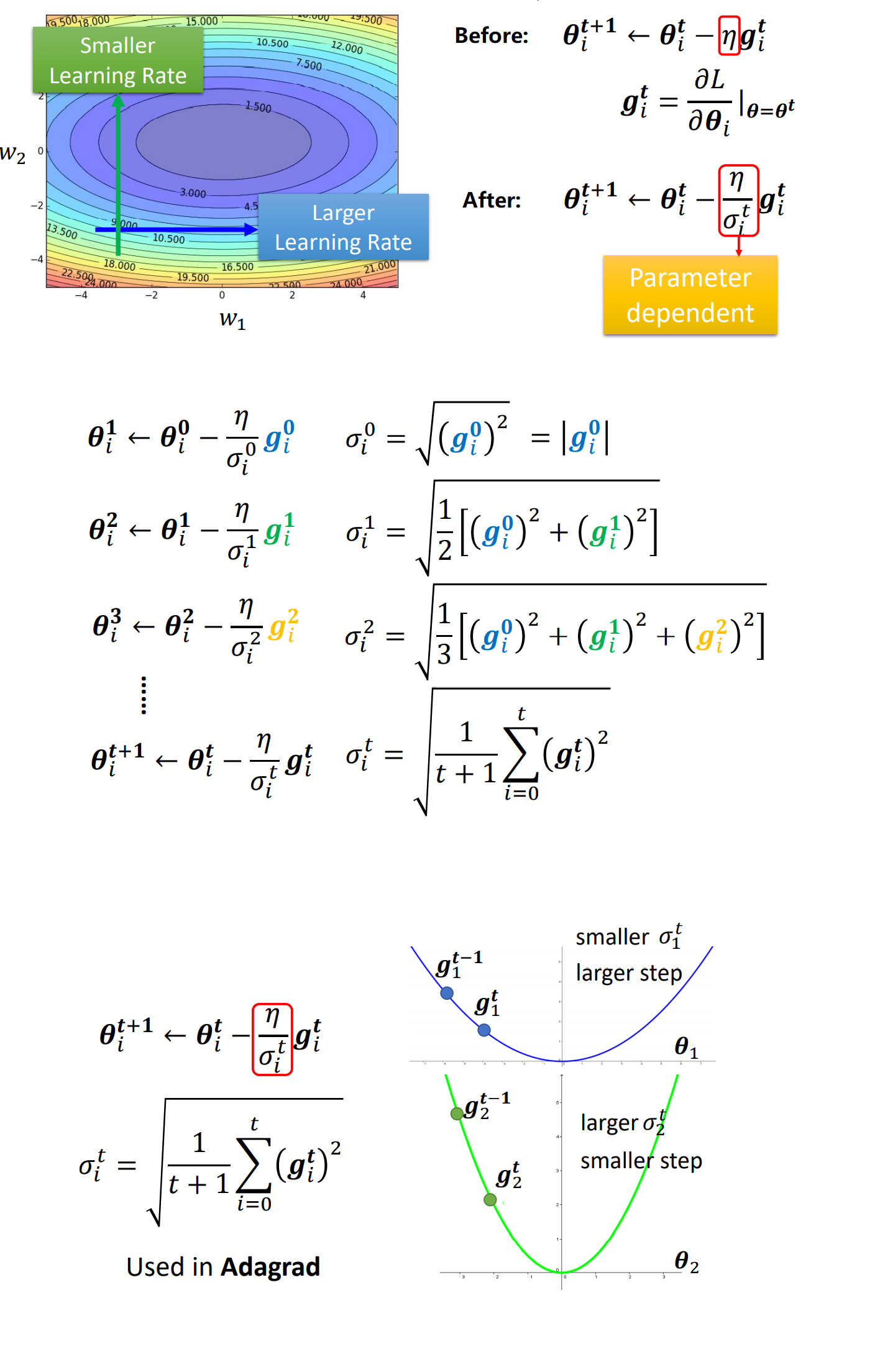
RMSProp
为了让Learning Rate有更好的弹性,我们对Adagrad进行了改进,我们利用RMSProp方法,让Learning Rate在平缓的地方下降的更快,陡峭的地方下降的更慢。

- 问题: 长时间只在某个维度下降,可能导致在另一个维度上LearningRate骤增。
当长时间在只在某个方向上进行梯度下降,可能会导致另一个维度上LearningRate骤增,这时候会出现下图中的问题:
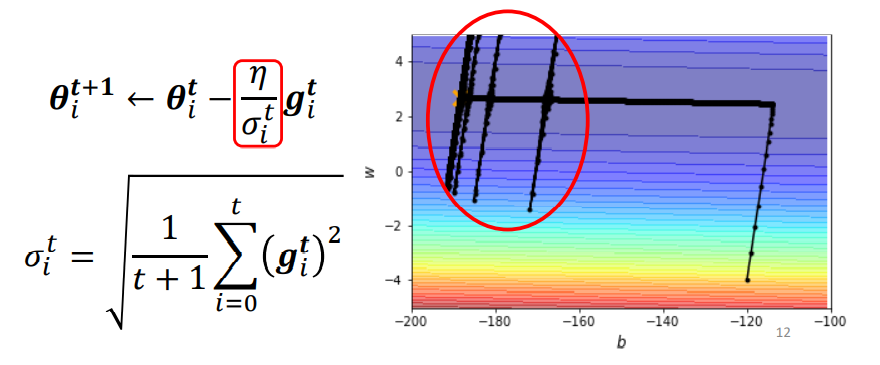
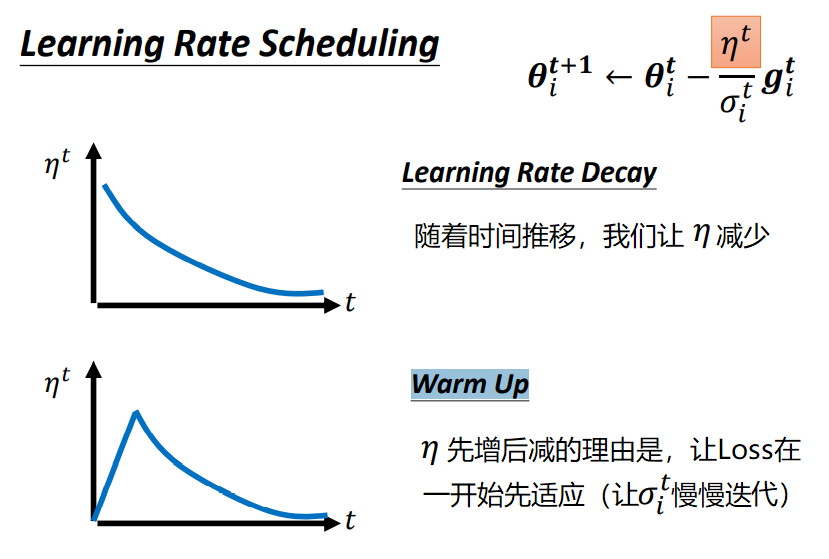
为了应对这样的问题,我们通常有两种方式处理:
- Learning Rate Decay
- Warm Up
Adam (RMSProp + Momentum)
Adam是对之前所有梯度下降算法的一次集大成,是目前较为广泛应用的梯度下降算法,代替了Adagrad和RMSProp的使用。

BatchSize
DNN的训练过程中,往往是将Training Set划分为各块Batch,各块进行梯度下降。 所以更新的次数Update = Epochs / BatchSize。
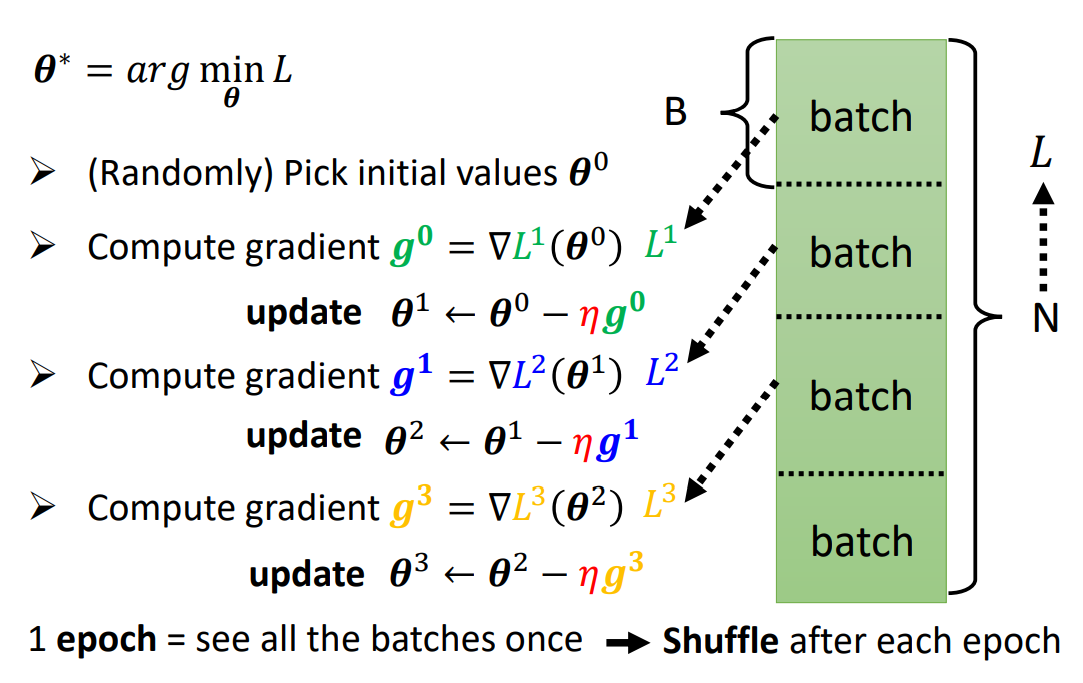
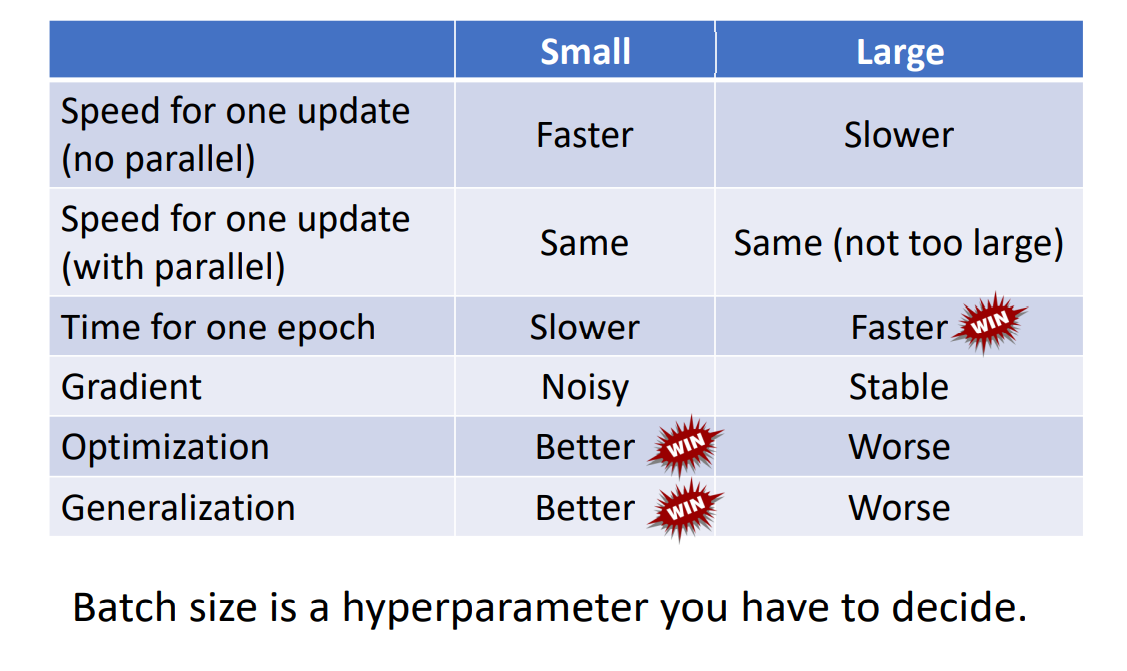
需要注意的是,更小的Batch往往不能在CPU/GPU上更好的并行运算,所以下降运算速度会比较大的Batch慢。
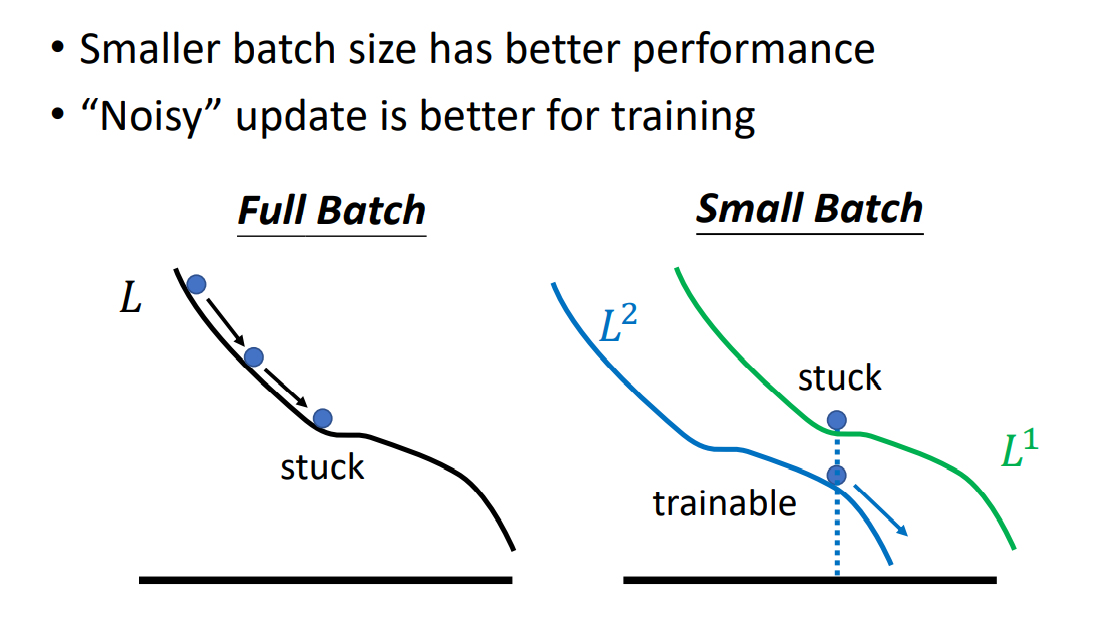
但是,在每一次下降中,都会对应不同的Loss函数曲线,这样在真正分布的Loss上进行梯度下降会产生Noisy噪声,它的正是在于不容易卡在Critical Point上。
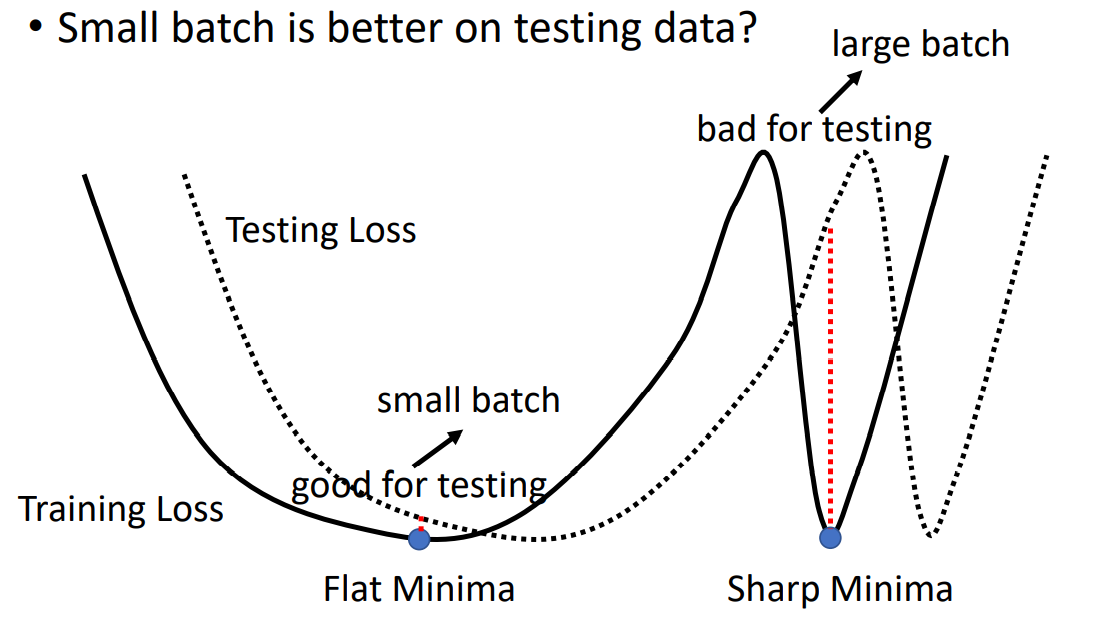
其实,更小的Batch甚至可以在Testing Set上获得不错的表现。解释这个现象需要注意的是,不同的local minima就算可使Loss相等,也是有好坏之分的。 在Training Set上,相同的local minima中,开口越平缓(二阶导数越小)的local minima会更好。因为相对于在Testing Set上,其Loss曲线往往和Training Set的Loss曲线不完全一致,但相接近。此时,平缓的local minima有更好的容错区间,下图阐释了这样的现象:
接下来,我们对Small Batch v.s. Large Batch进行总结比较:
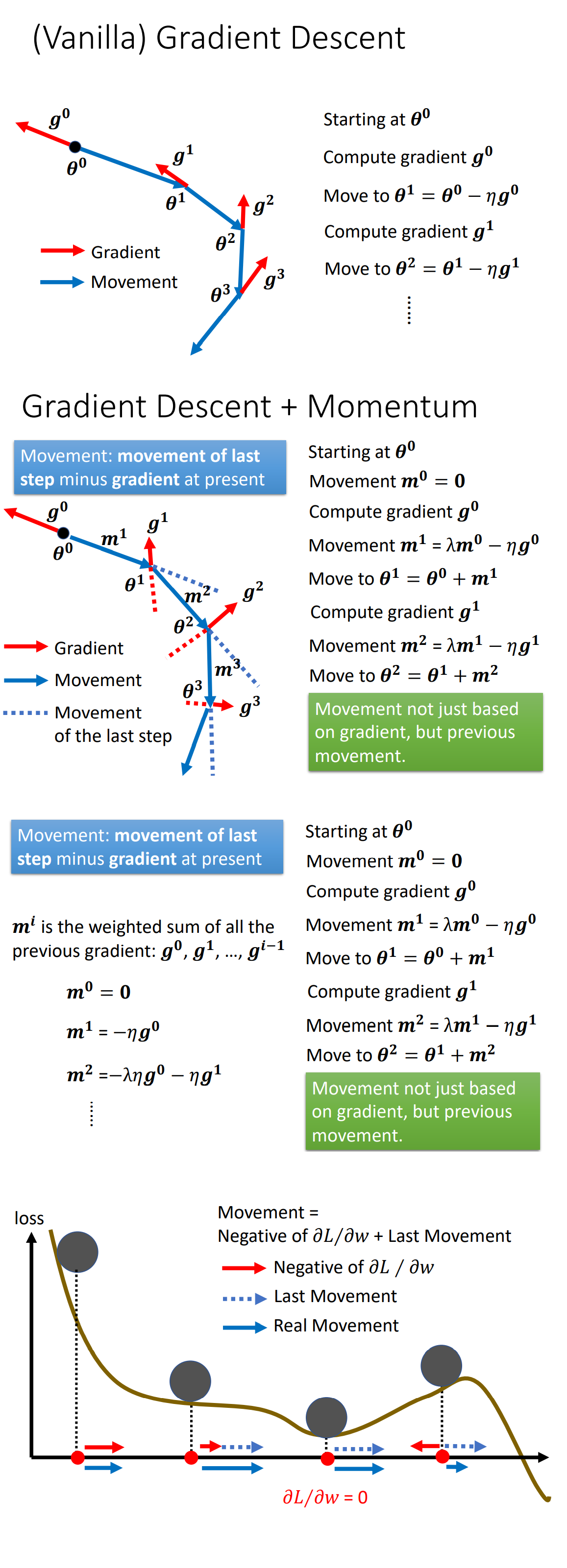
Momentum
Momentum就是为梯度下降增加惯性,使其下降的过程更富有物理弹性。
经过一系列的优化改进,我们可以最终把Gradient Descent理解成如下公式: