机器学习任务概述 ML Guideline
机器学习的训练步骤
- Step 1: function with unknown
- Step 2: define loss from training data
- Step 3: optimization

函数式Function
函数分类
- Regression: 输入1个向量,输出1个向量(连续的值)
- Classification: 输入1个向量,输出1个向量(离散的值)
- Seq2Seq: 输入N个向量,输出M个向量(输入的向量间有关联)
- Structured Learning: 创造含有结构的文档、图片、音乐等
参数术语
例如,对于一个基础的线性模型Linear Model,其Function可以表示为:
$y = b + (w_1,…,w_n)^T (x_1,…,x_n)=b+WX$
对于上述式子,则可以称:
- X: 特征(feature)
- W: 权重(weight)
- b: 偏置(bias)
- $\theta$: $(W,b)^T$等构成的向量
传统的线性回归模型,为了实现简单的非线性化,可以通过Basis Function实现:
$y=b+W·\phi(X)$
其中可以称$\phi(X)$为基函数,常见的基函数有:
- 多项式基函数:$\phi(X)=\sum_{i=1}^n x_i^i$
- 高斯基函数:$\phi(X)=\sum_{i=1}^n e^{-\frac{(x_i-\mu_i)^2}{2s^2}}$
激活函数
在机器学习中,为了拟合非线性的分布曲线,通常需要通过多个激活函数进行叠加,常见的激活函数有:
- Sigmoid: $\sigma(x) = \frac{1}{1+e^{-x}}$
- ReLU: $\sigma(x) = max(0, b+wx)$
- Maxout: $\sigma(x) = max(b_1+w_1 x, b_2+w_2 x)$
损失函数Loss
损失函数表示了当前模型在某个数据集合上的质量,因此损失函数Loss是一个含参函数。对于一般的Linear Model,可以定义其损失函数为:
-
MAE(Mean Absolute Error): $L(\theta) = \frac{1}{n} \sum_{i=1}^n \mid y_{\theta}(X_i) - \hat{y} \mid$
-
MSE(Mean Square Error): $L(\theta) = \frac{1}{2n} \sum_{i=1}^n (y_{\theta}(X_i) - \hat{y})^2$
-
RMSE(Root Mean Square Error): $L(\theta) = \frac{1}{n} \sqrt{ \sum_{i=1}^n (y_{\theta}(X_i) - \hat{y})^2 }$
-
CrossEntropy(Always Used in Classification): $L(\theta) = \frac{1}{n} \sum_{i=1}^n ( \sum_{j=1}^m -\hat{y_j^i} \ln{y_\theta(X_j^i)} )$
需要注意的是,为了方便梯度下降求微分,MSE和RMSE最好再乘上$\frac{1}{2}$。
其中Regression回归任务多使用MSE作为损失函数,而Classification分类任务多使用CrossEntropy交叉熵作为损失函数。
优化器Optimization
优化器Optimization的任务是使损失函数Loss尽可能地小。常见的优化器就是梯度下降(Gradient Descent)算法系列。
梯度下降的目标在于:$\theta^* = argmin {L(\theta)}$,其步骤如下:
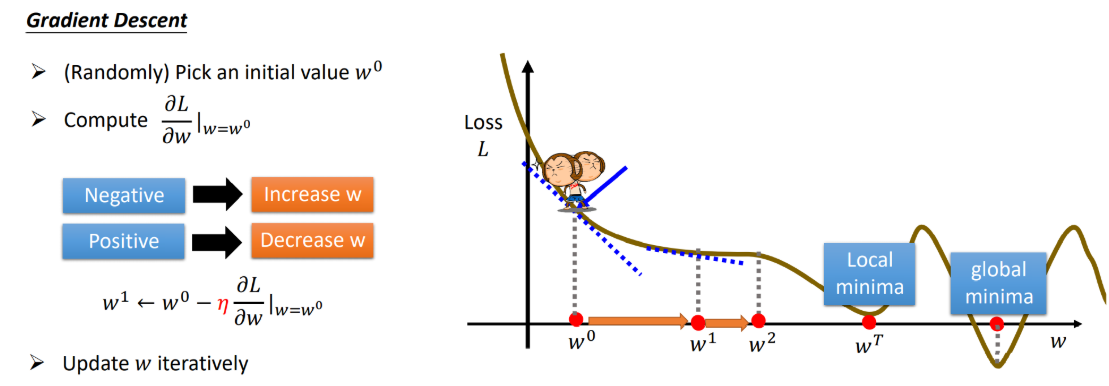
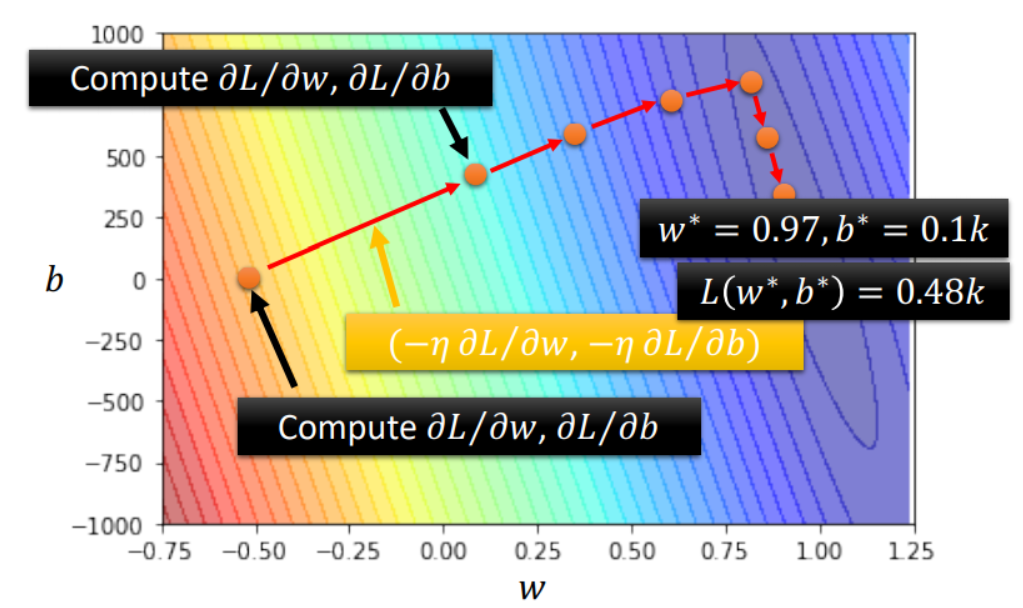
其中,梯度下降的基本方程是:$\theta^{t+1} \gets \theta^{t} - \eta * \nabla L(\theta^t)$
下降结果(Critical Point)
- Local Minima: 局部最小值
- Saddle Point: 鞍点(各方向的微分为0,但仍具有下降可能)
Gradient Descent分类
- VGD(Vanilla Gradient Descent): 一般的梯度下降法
- MBGD(Mini-Batch Gradient Descent): 小批量梯度下降法
- SGD(Stochastic Gradient Descent): 随机梯度下降法
- Adagrad: 学习率自适应的梯度下降法
- RMSProp: 改进的学习率自适应的梯度下降法
- Adam(RMSProp + Momentum): 自适应稳定梯度下降算法