机器学习任务攻略 ML Recipe
问题分析
分析模型在训练集和测试集的表现时,常见的策略如下为:
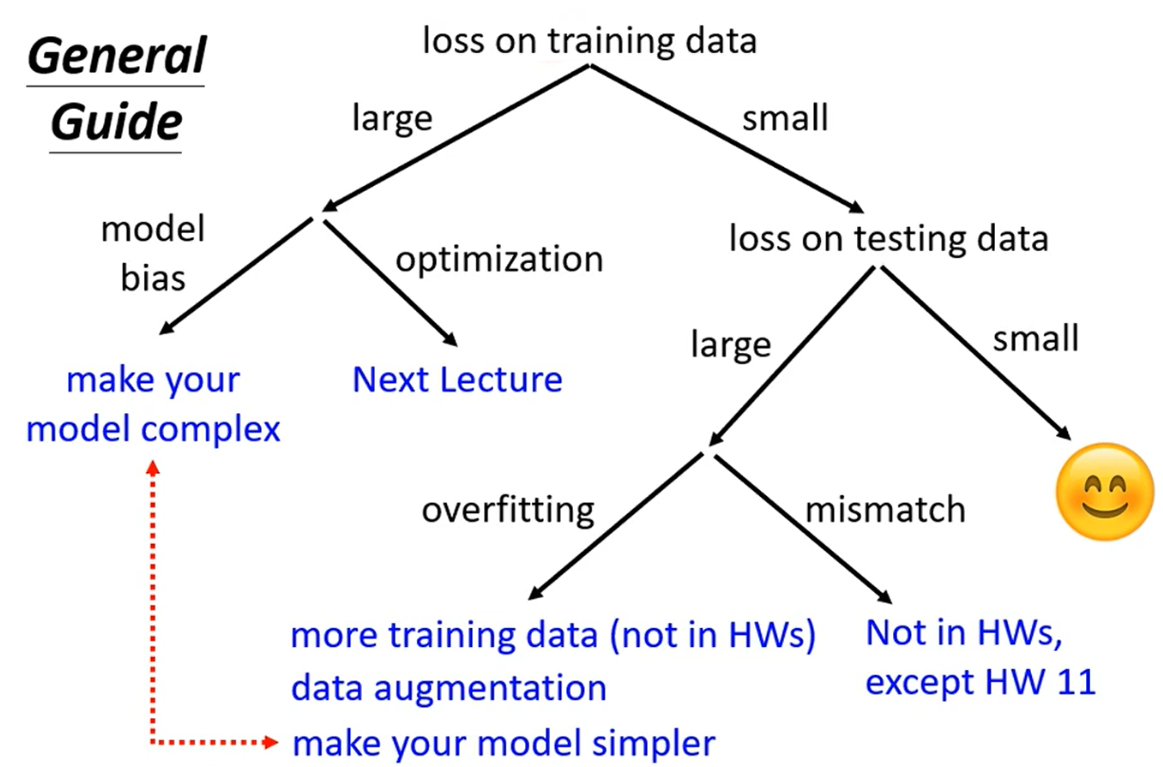
训练集TrainingSet表现差
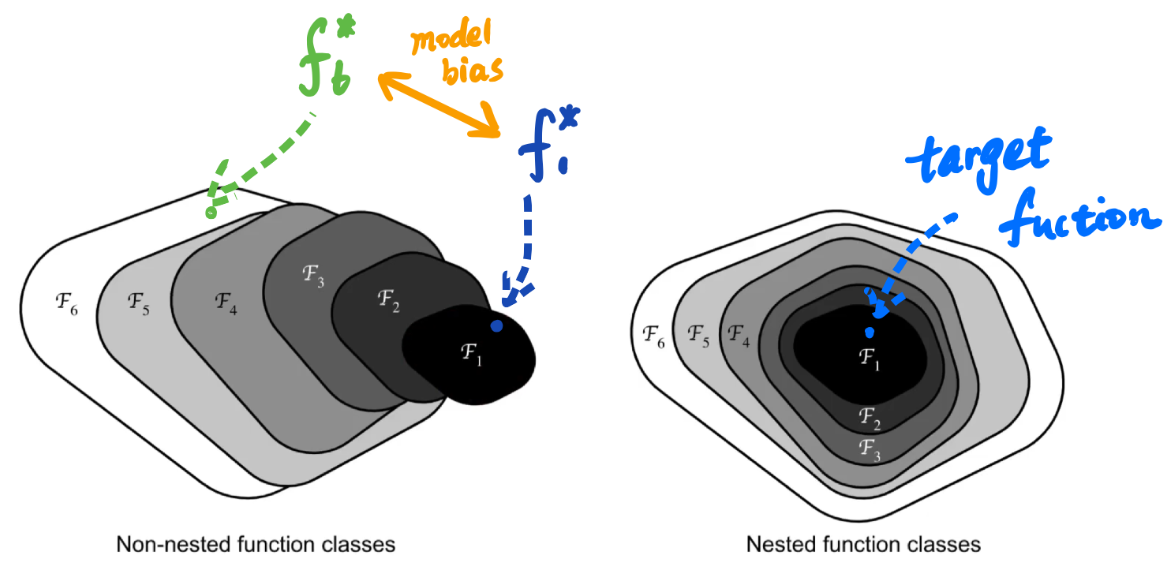
1.模型过于简单(Model Bias)
形象的讲就是:在大海里捞针,针不在大海里; 常见的策略是让模型变得复杂化,使可以得到的Function中能够有一个符合较低的Loss

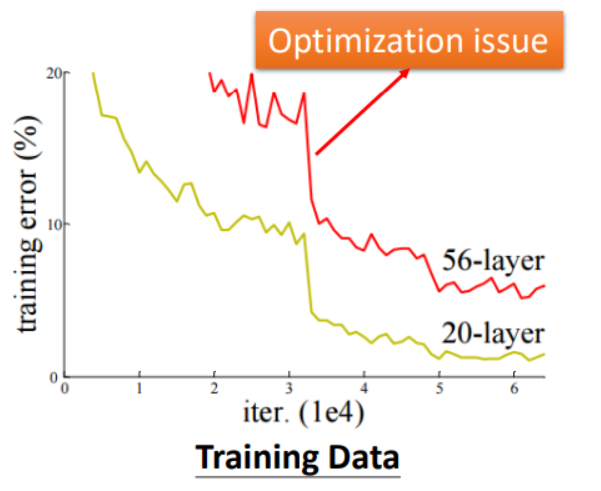
2.优化器做的不够好(Optimization)
形象的讲就是:在大海里捞针,针就在大海里,但却捞不到;这是往往需要对Optimizer进行优化,例如SGD中调整LR或Monument等超参数。

通常解决这样的方法就是将SGD随机梯度下降改为Adam并设置weight_decay作用L2正则化。
3.模型过于复杂(Model Bias)
形象的讲就是:在大海里捞针,但不知道在哪片海;在CNN卷积影像识别领域中,可以利用ResNet残差网络进行优化解决。
因此,当我们遇到训练的模型在训练集上表现差时,可以试着以下策略:
- 用一个比较简单的Model在训练集上进行训练,得到最终的损失Loss 0;
- 用一个较为复杂的Model在训练集上进行训练,得到最终的损失Loss 1;
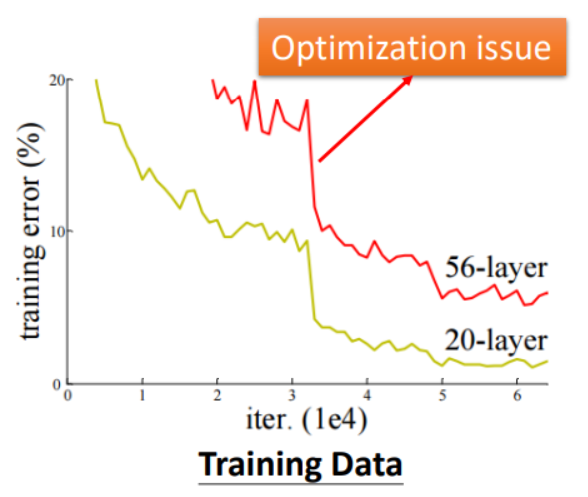
如果Loss 1并没有比Loss 0增加很多,则考虑是Optimization出现问题,反之就是Model的复杂度不够高。
但是也要注意,当模型复杂度过高的时候,也会出现问题。假设梯度下降不存在问题,在测试集的损失Loss未必会随着模型复杂度增加而减少(过拟合Overfitting问题)。
测试集Testing Set表现差
通常在训练集上表现得不错,但在测试集却表现的不尽人意,则可以称为过拟合Overfitting问题
解释过拟合,举个极端的例子如下:

过拟合问题中,可能是因为我们的模型过于弹性,会出现如下问题:
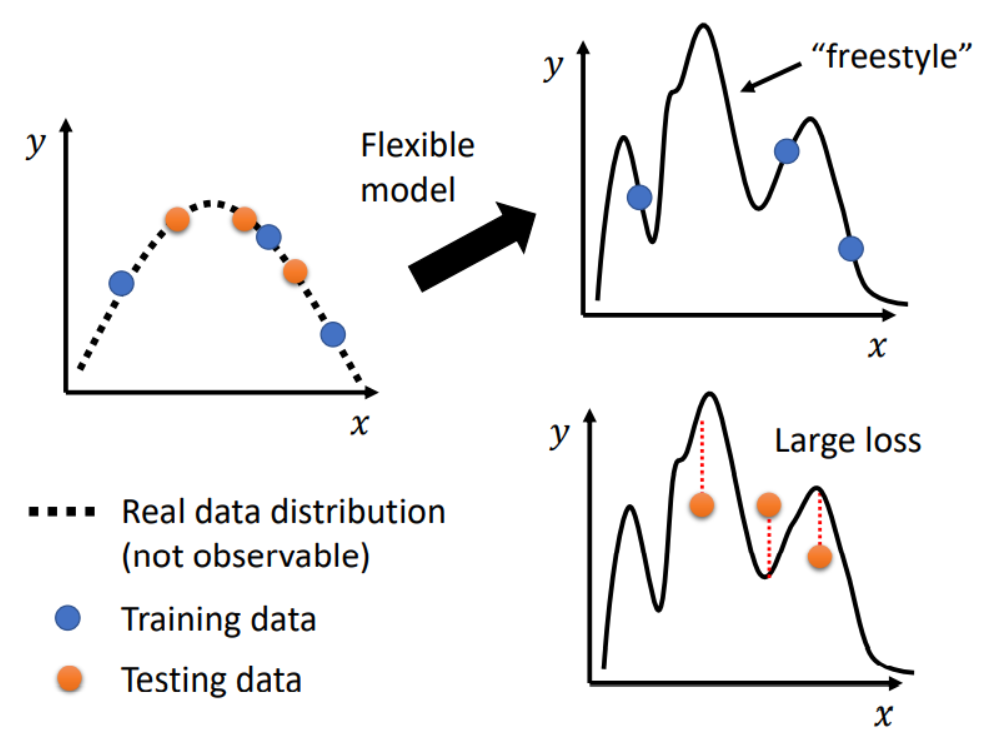
应对的策略可以是,基于我们的Domain Knowledge领域知识,自己设计测试样例训练模型。
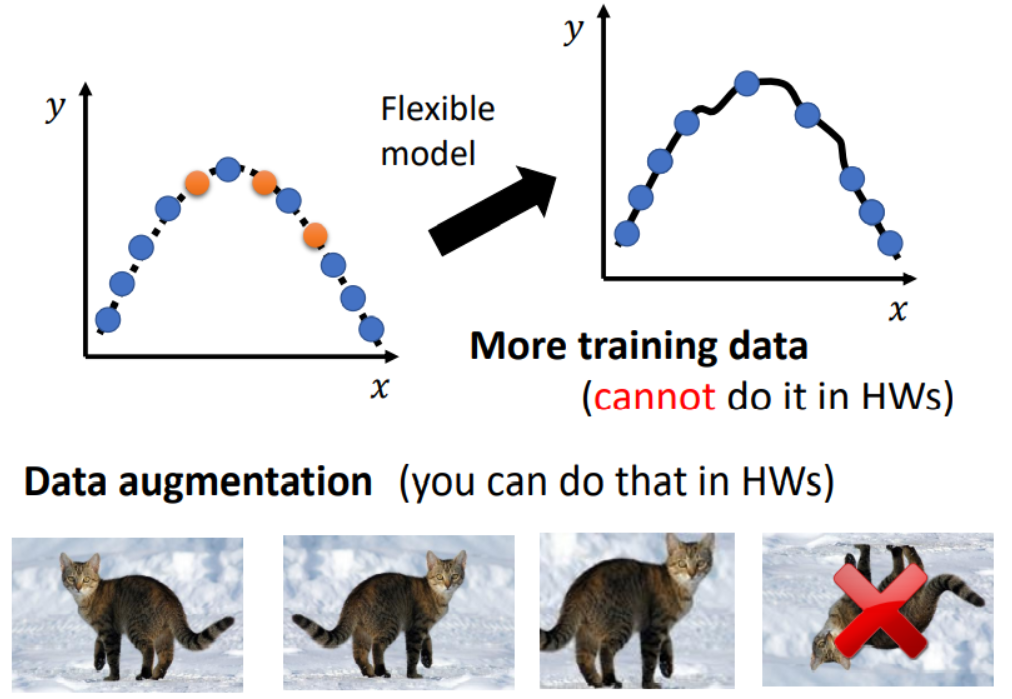
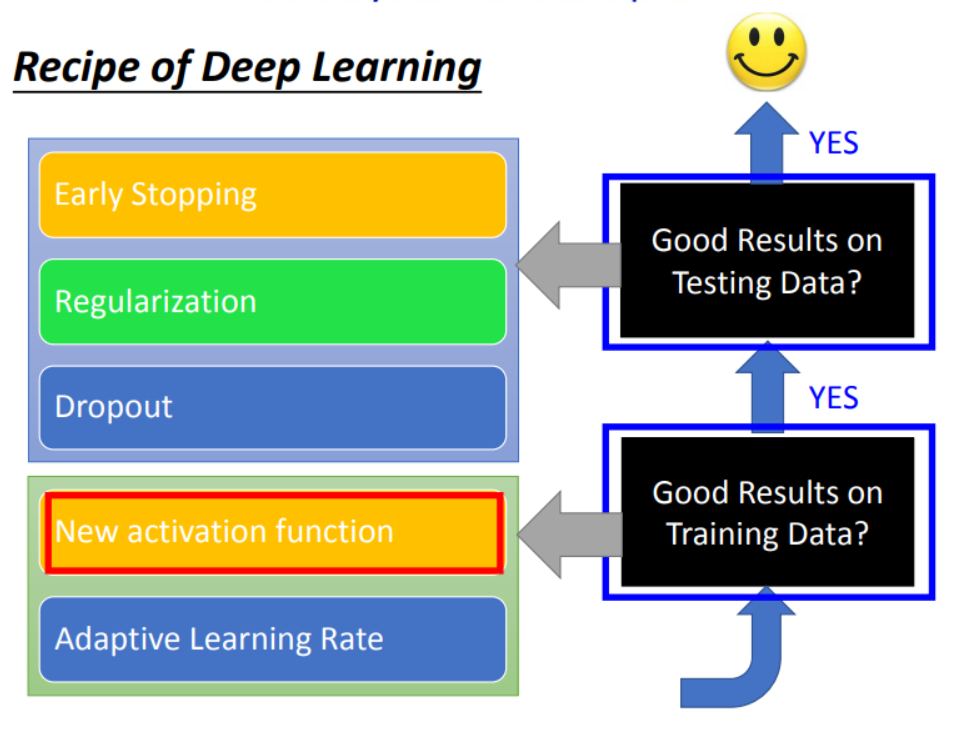
其他的策略还有:
- less / share parameter: 共享参数(例如CNN中利用神经元解释卷积过程)
- less feature: 减少特征类型带来的影响
- early stopping: 避免过拟合现象
- normalization: 归一化(例如特征归一化等)
- regularization: 正则化(例如L2正则,让下降更平缓)
- dropout: 训练时让某层的神经元以某种概率随机失效
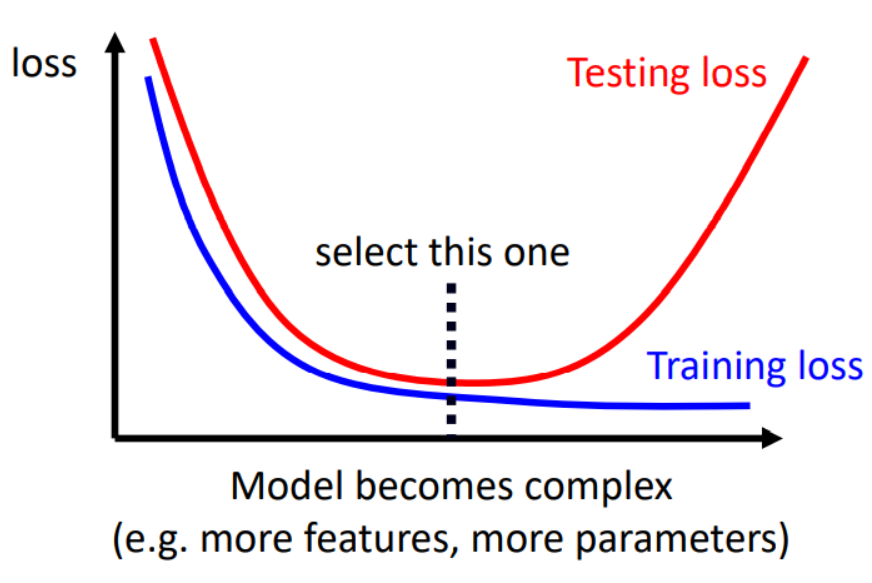
另外,附上模型复杂度和模型在测试集上的关系图。
策略手册
调整训练集的总量、特征数量
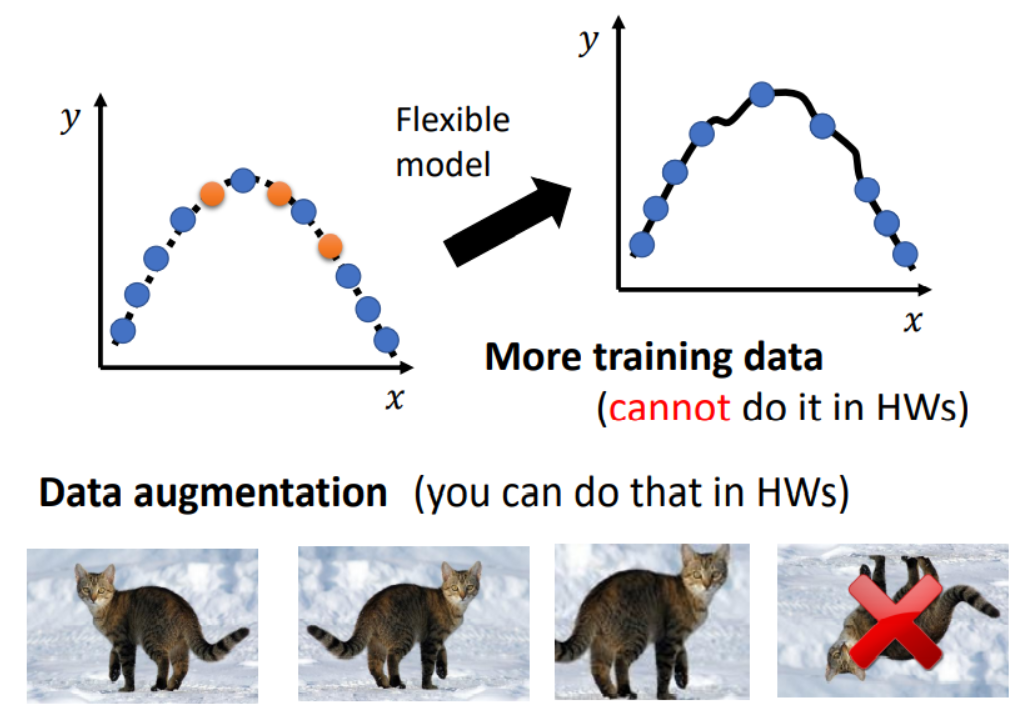
Data Augmentation
通过Data Augmentation在原数据集上增量,常见的例如CNN中对图片进行放大。
Semi-Supervisor
利用半监督学习Semi-Supervisor,在训练过程中增加训练集的数据量。
例如在Classification分类任务中,每个训练迭代器寻找softmax后预测概率超过特定阈值的数据用于下一轮训练。
Feature Engineering
对特征features数量进行增加或删除。
Feature Normalization
采用Feature Normalization特征归一化。

模型Function/Model改进
Deep Neural
调整神经网络的深度和大小,通常小模型=>大模型进行测试。
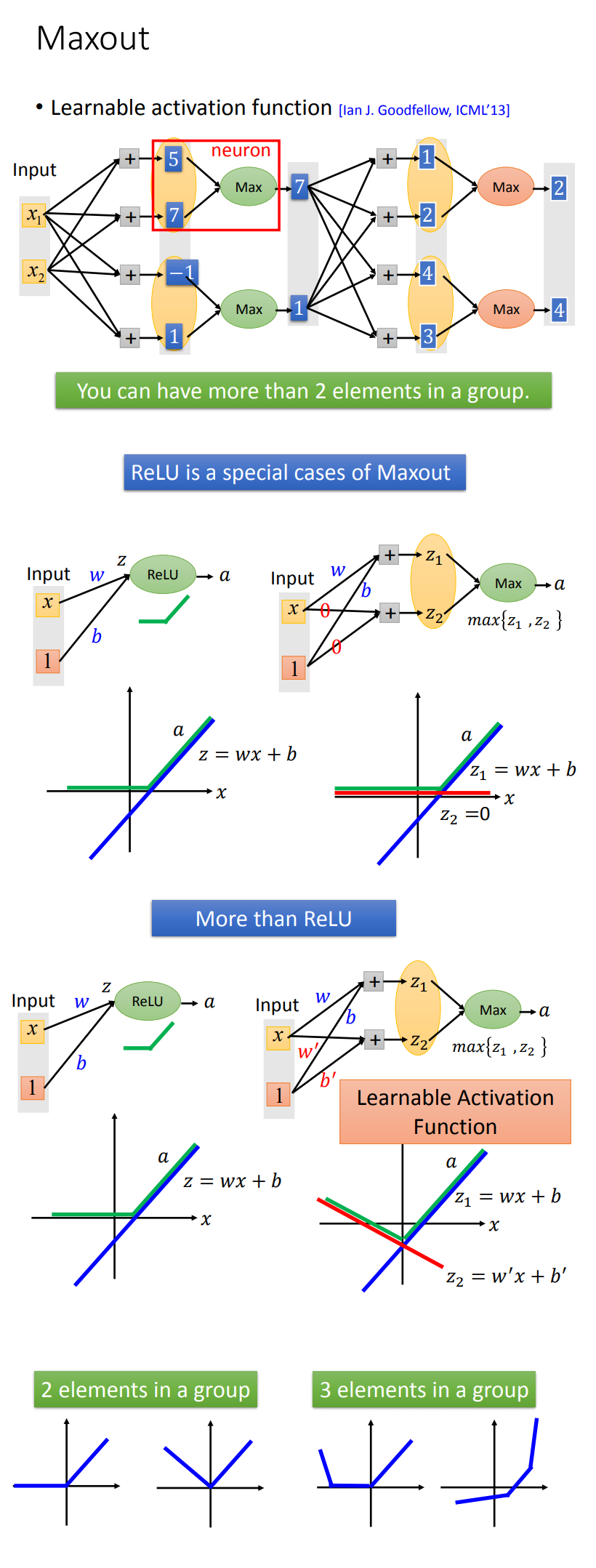
Activation Function
调整激活函数Activation Function,常见的激活函数:
- Sigmoid: $\sigma(x) = \frac{1}{1+e^{-x}}$
- ReLU: $\sigma(x) = max(0, b+wx)$
- Maxout: $\sigma(x) = max(b_1+w_1 x, b_2+w_2 x)$
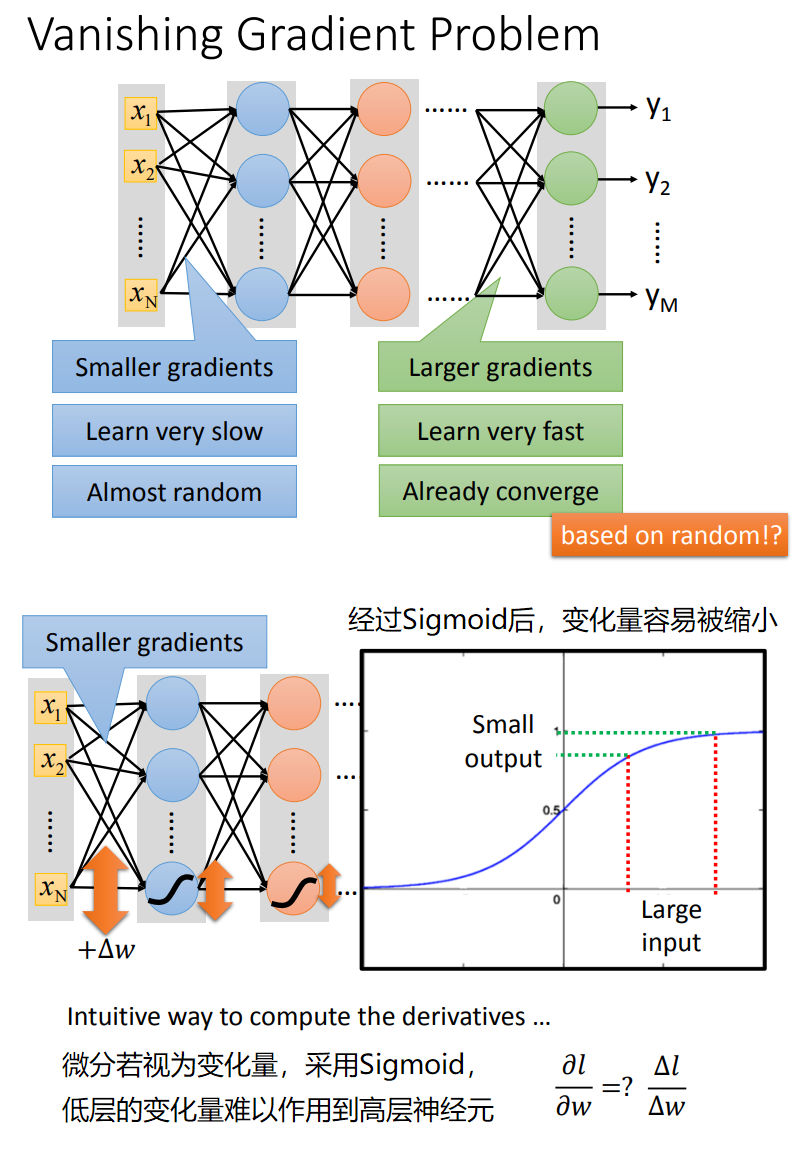
Sigmoid在深度神经网络中,具有明显的缺陷,及离输出层越远的神经元,越难被更新到,有时训练结束后,离输出层较远的神经元权值可能仍然是随机的。
ReLU是深度神经网络中,最常用的激活函数,它克服了Sigmoid的一些问题。
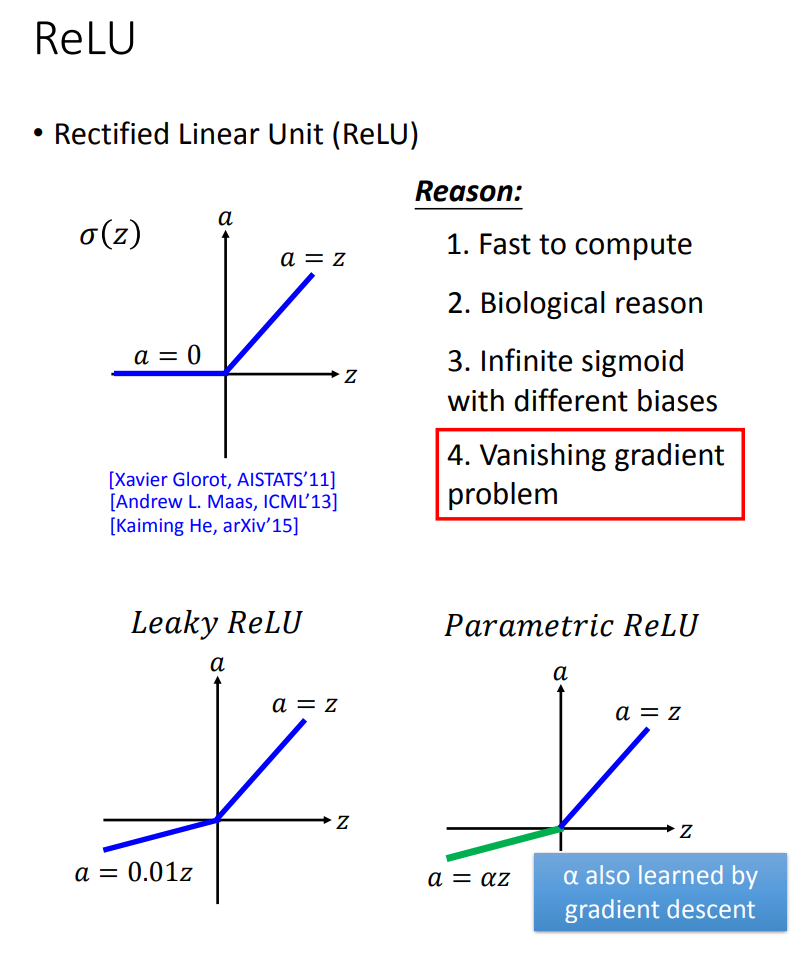
当然,也可以引入自学习的Activation Function,这就是常用的Maxout激活函数,通常可以认为,ReLU就是Maxout的一种特例。
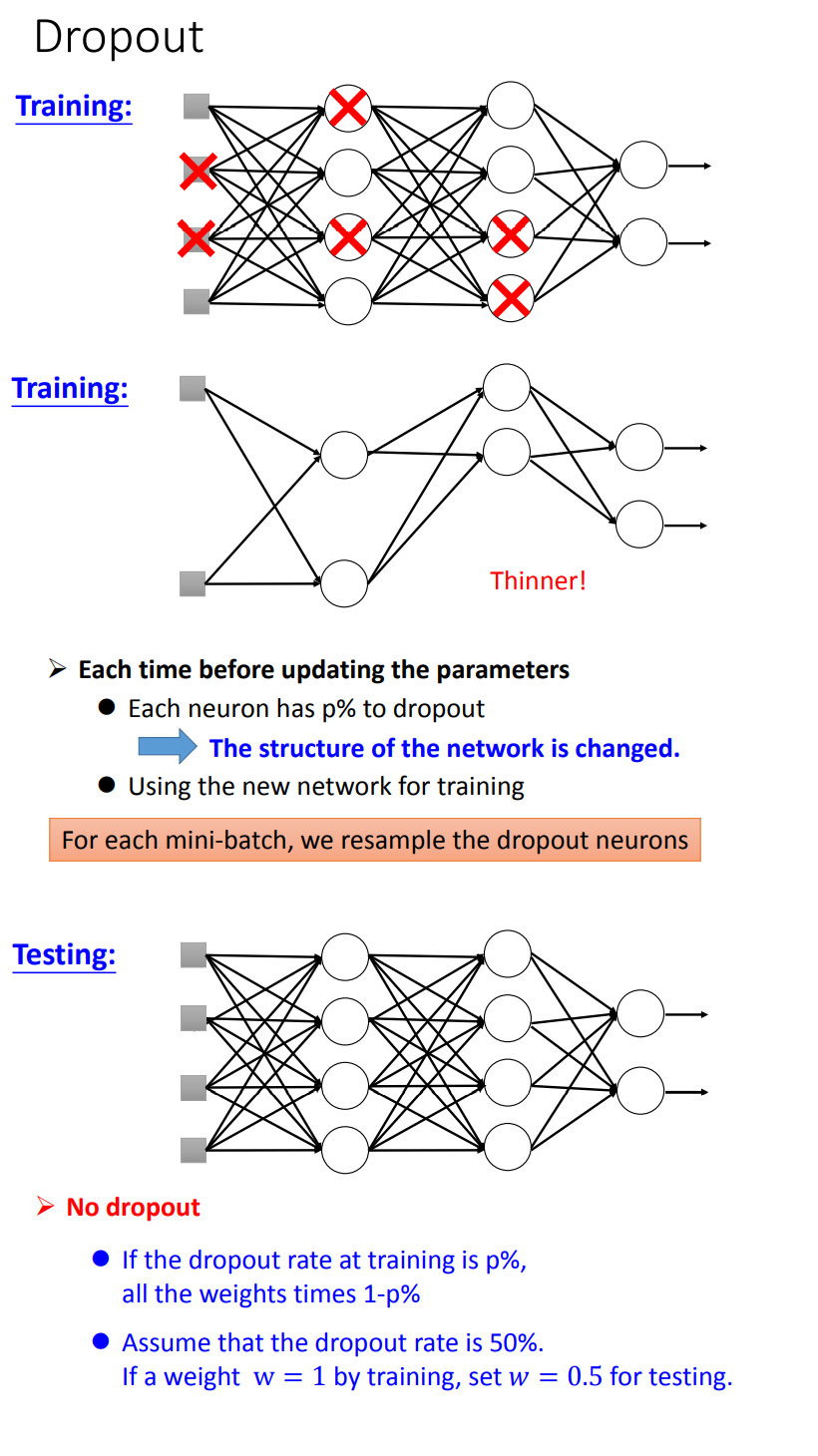
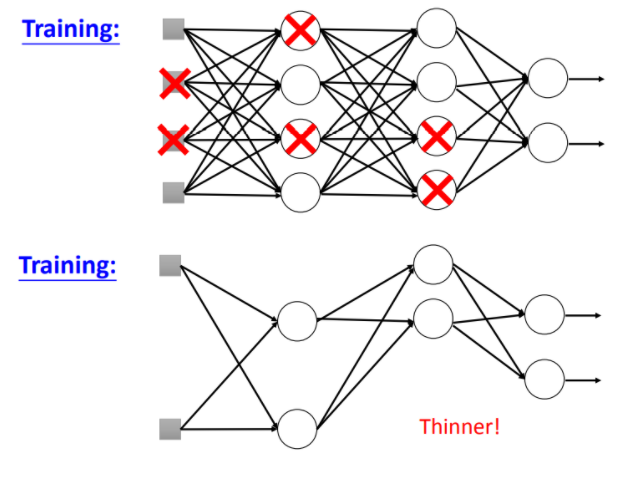
Dropout
Dropout在每一层中以概率$p$随机使某些神经元失效,使得神经网络更加thinner。
- 训练时
model.train(),以概率$p$使某些神经元失效;- 测试时
model.eval(),以概率$1-p$乘上每个神经元的权重;
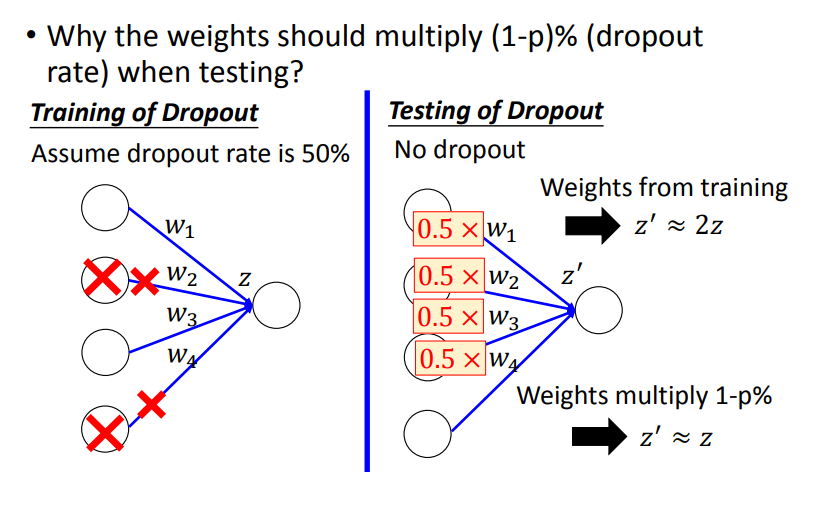
之所有要在测试时,乘上$1-p$的原因是在验证时,相比于训练时是所有神经元参与工作。
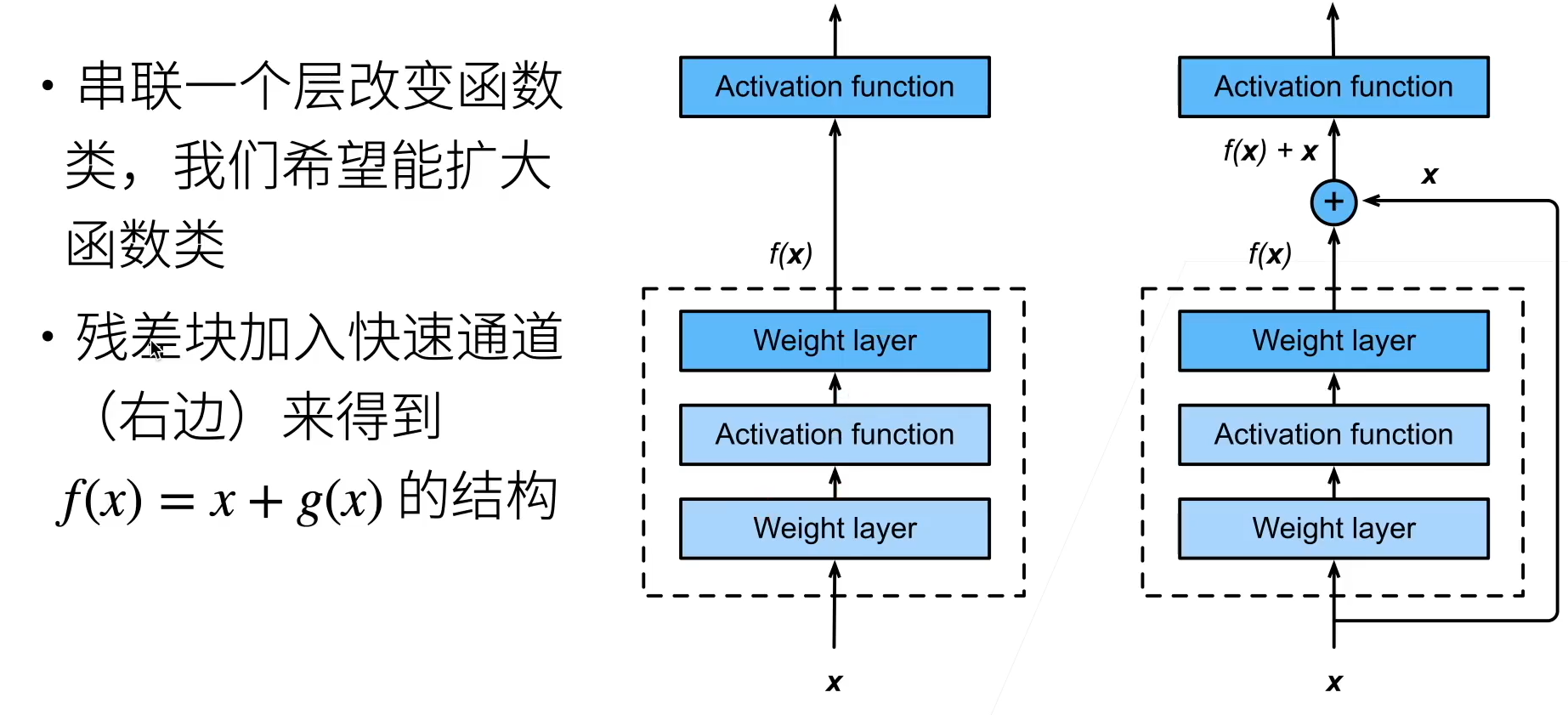
Residual Block
将神经网络拆分成Block块,每个块到下一个块的路径有两条,一条是经过神经网络后到达,另一条路径是输入向量直接到达下一个残差块。将两条路径输出的向量拼接到一个向量传递到下一个Block。以此可以消除Model Bias的问题。残差块的应用如ResNet,在加深神经网络的时候,解决网络退化的问题。关于ResNet和Residual Block的理解可以参照李沐ResNet讲解。
损失函数Loss改进
Loss Function
选择合适的Loss Function
- Regression : MSE / RMSE
- Classification: CrossEntropy
Regularization正则化
L2正则化可以使Loss损失函数下降的更加平缓,不容易出现过拟合的现象。

可以想象一下采用了L2正则化的函数,在下降过程中,某些权重weight会更快的下降到趋近于0,这使得在梯度下降过程中越接近0的权重更快的向0迭代,从而导致某些神经元被淘汰,因此对模型进行了适当的缩小,不容易出现过拟合问题。
优化器Optimization改进
Learning Rate & Momentum
使用SGD时,可以对learning rate和momentum进行优化,其两参数的具体数学含义可以见梯度下降介绍。
learning rate <= 0.01
momentum = 0.8 ~ 0.9
Adam
在SGD不能给出比较好的下降效果时,可以考虑使用Adam进行自适应的learning rate下降。
训练过程Training Process改进
Epochs & BatchSize
调整epochs迭代次数以及batch size批大小
通常epochs的次数不易过大,否则会出现过拟合问题;
对于Batch Size,即在某次迭代中,取一定尺寸的批数据进行梯度下降。
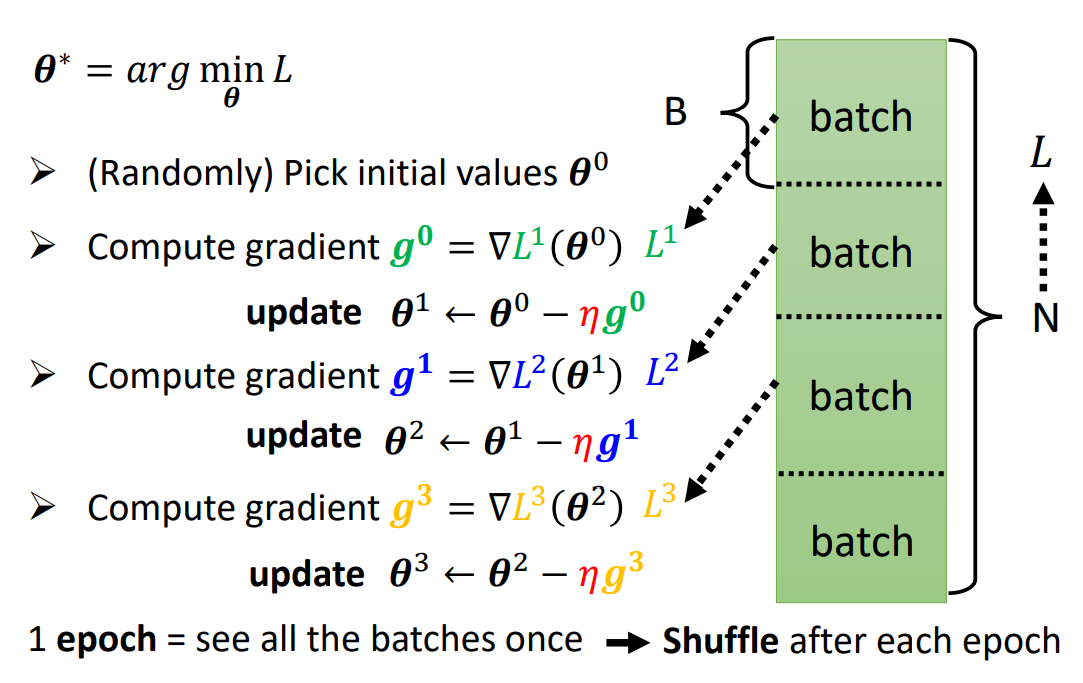
需要注意的是,更小的Batch往往不能在CPU/GPU上更好的并行运算,所以下降运算速度会比较大的Batch慢。
但是,在每一次下降中,都会对应不同的Loss函数曲线,这样在真正分布的Loss上进行梯度下降会产生Noisy噪声,它的正是在于不容易卡在Critical Point上。
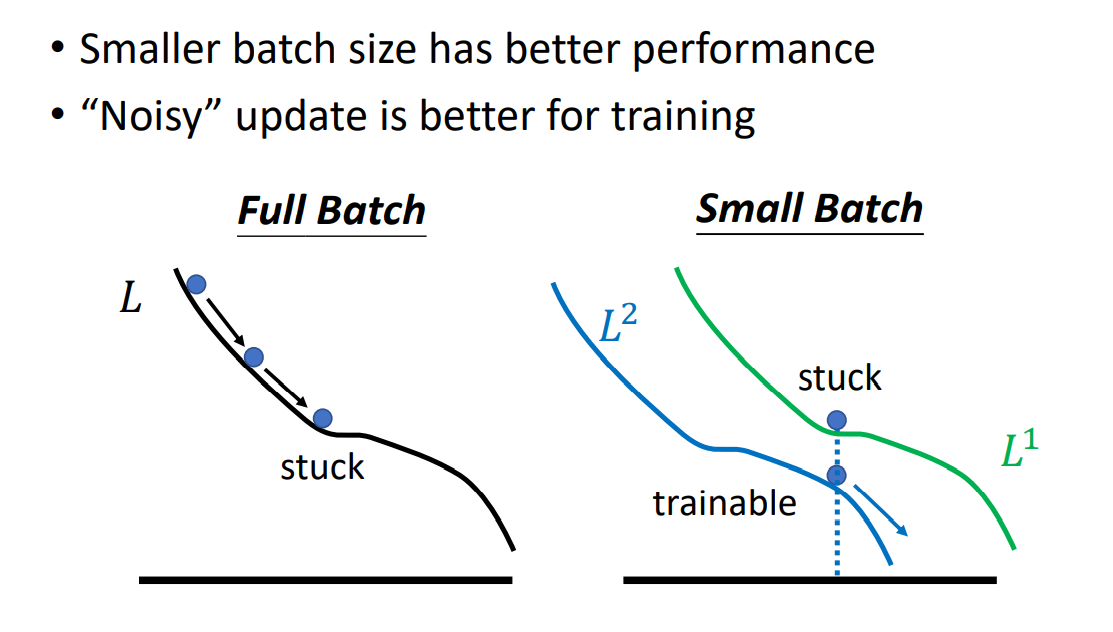
其实,更小的Batch甚至可以在Testing Set上获得不错的表现。解释这个现象需要注意的是,不同的local minima就算可使Loss相等,也是有好坏之分的。 在Training Set上,相同的local minima中,开口越平缓(二阶导数越小)的local minima会更好。因为相对于在Testing Set上,其Loss曲线往往和Training Set的Loss曲线不完全一致,但相接近。此时,平缓的local minima有更好的容错区间,下图阐释了这样的现象:
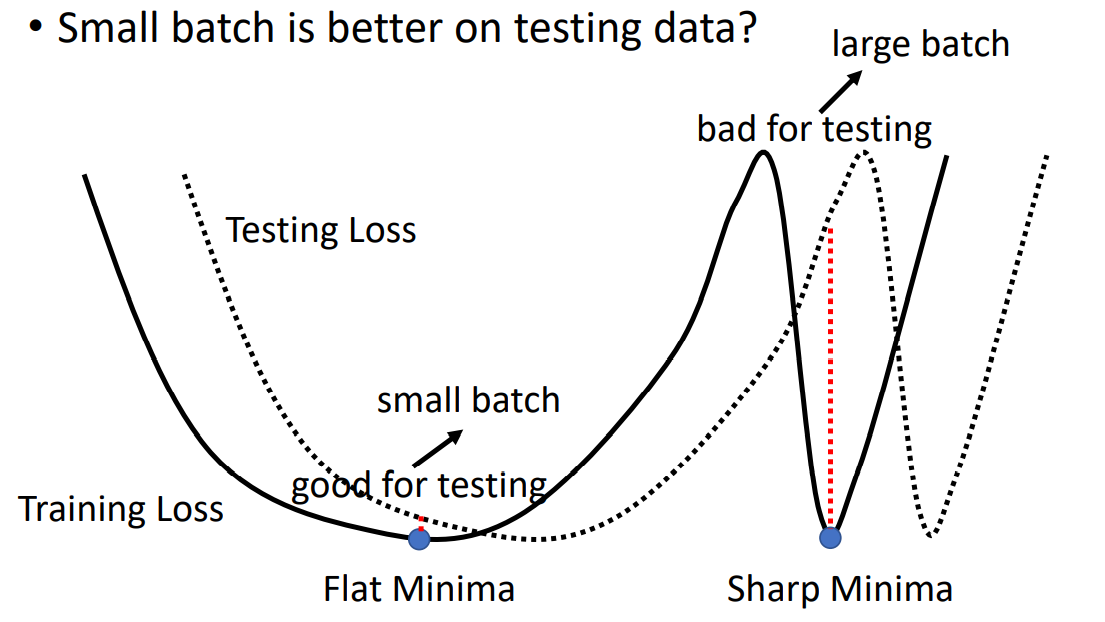
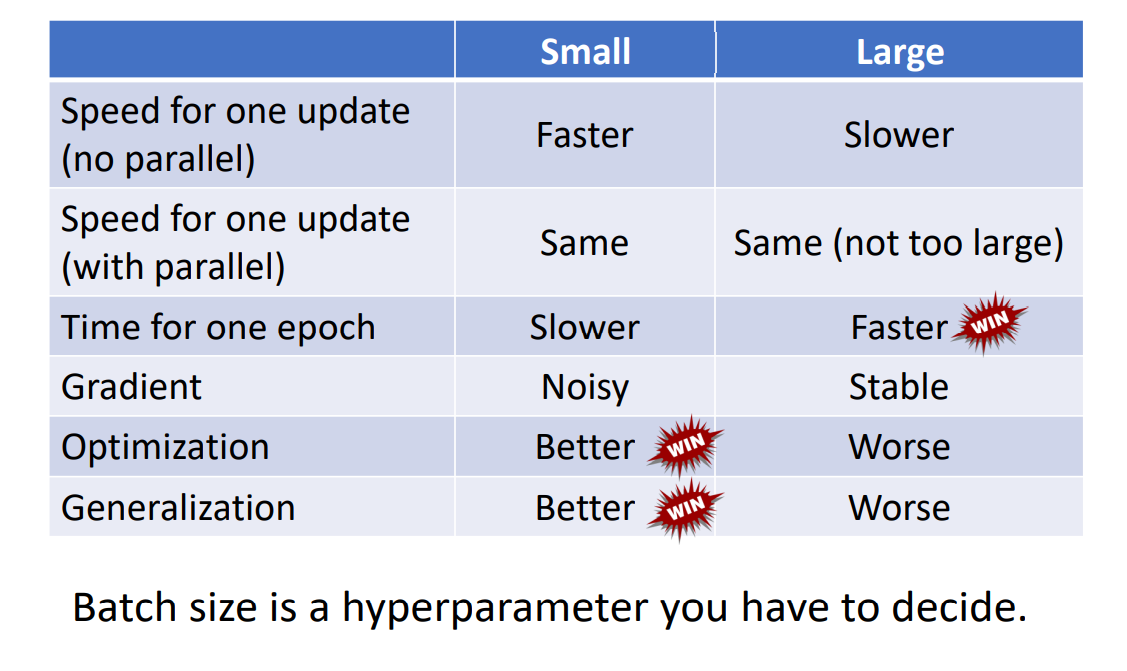
接下来,我们对Small Batch v.s. Large Batch进行总结比较:
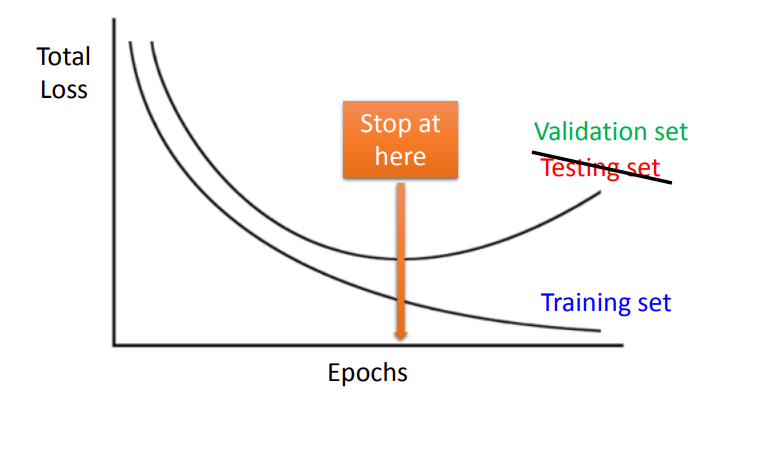
early-stop
通常在训练迭代过程中,为了防止过拟合Overfitting,可以在验证集损失持续某段时间后立即终止迭代。